Vecteurs colinéaires
Définition :
Deux vecteurs non nuls \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires lorsqu'il existe un réel t tel que \(\overrightarrow{v}=t.\overrightarrow{u}\).
Par convention, le vecteur nul \(\overrightarrow{0}\) est colinéaire à tous les vecteurs.
Remarque :
Deux vecteurs colinéaires non nuls ont la même direction.
Si \(\overrightarrow{v}=t \overrightarrow{u}\) avec \(t>0\), alors \(\overrightarrow{u}\) et \(\overrightarrow{v}\) ont le même sens.
Si \(\overrightarrow{v}=t\overrightarrow{u}\) avec \(t<0\), alors \(\overrightarrow{u}\) et \(\overrightarrow{v}\) ont le sens contraire.
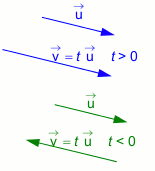
Complément :
Lorsque deux vecteurs non nuls sont colinéaires, on dit qu'ils sont dépendants. Dans le cas contraire, on dit qu'ils sont indépendants ou libres.