Dans un tétraèdre
On considère un tétraèdre ABCD.
On appelle I,J,K et L les points définis respectivement par :
\(\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AB}\) ; \(\overrightarrow{BJ}=\dfrac{1}{3}\overrightarrow{BC}\) ; \(\overrightarrow{CK}=\dfrac{2}{3}\overrightarrow{CD}\) ; \(\overrightarrow{DL}=\dfrac{1}{3}\overrightarrow{DA}\)
Question
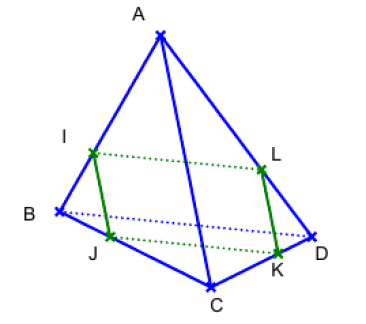
Placer les points I,J,K et L sur une figure.
Question
Exprimer \(\overrightarrow{IJ}\) en fonction de \(\overrightarrow{AB}\) et \(\overrightarrow{BC}\), puis en fonction de \(\overrightarrow{AC}\).
Indice
On pourra remarquer que \(\overrightarrow{IJ}=\overrightarrow{IA}+\overrightarrow{AB}+\overrightarrow{BJ}\)
Solution
\(\overrightarrow{IJ}=-\overrightarrow{AI}+\overrightarrow{AB}+\overrightarrow{BJ}\)
Donc \(\overrightarrow{IJ}=-\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{BC}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{BC}\)
En factorisant et en utilisant la relation de Chasles, on peut simplifier l'écriture de \(\overrightarrow{AI} \):
\(\overrightarrow{IJ}=\dfrac{1}{3}(\overrightarrow{AB}+\overrightarrow{BC})=\dfrac{1}{3}\overrightarrow{AC}\)
Question
Justifier que les points I,J,K et L sont coplanaires et que la droite (AC) est parallèle au plan (IJKL).
Indice
On pourra exprimer \(\overrightarrow{LK}\) en fonction de \(\overrightarrow{AC}\).
Solution
\(\overrightarrow{LK}=\overrightarrow{LD}+\overrightarrow{DC}+\overrightarrow{CK}\)
Donc \(\overrightarrow{LK}=-\dfrac{1}{3}\overrightarrow{DA}+\overrightarrow{DC}+\dfrac{2}{3}\overrightarrow{CD}=\dfrac{1}{3}\overrightarrow{AD}+\overrightarrow{DC}-\dfrac{2}{3}\overrightarrow{DC}=\dfrac{1}{3}(\overrightarrow{AD}+\overrightarrow{DC})\)
Donc \(\overrightarrow{LK}=\dfrac{1}{3}\overrightarrow{AC}\).
En utilisant la question précédente, on en déduit que \(\overrightarrow{LK}=\overrightarrow{IJ}\) ce qui démontre que IJKL est un parallélogramme et donc que ces 4 points sont coplanaires.
On a vu que \(\overrightarrow{LK}=\dfrac{1}{3}\overrightarrow{AC}\) donc \((LK)//(AC)\).
La droite (AC) est parallèle à une droite du plan (IJKL) donc on peut affirmer que (AC) est parallèle au plan (IJKL).
Question
Démontrer que la droite (BD) est parallèle au plan (IJKL).
Solution
On raisonne de manière identique aux questions précédentes en montrant que \(\overrightarrow{JK}=\dfrac{2}{3}\overrightarrow{BD}\)
De là découle que \((JK)//(BD)\) et donc que (BD) est parallèle au plan (IJKL).