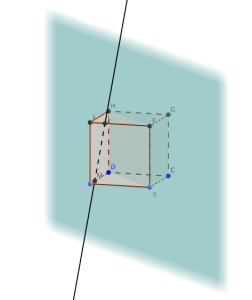
Démontrer le parallélisme d'une droite et d'un plan
Question
Montrer que \(\overrightarrow{ML}=\dfrac{1}{4}\overrightarrow{DB}+\overrightarrow{DH}\)
Indice
On pourra utiliser de manière astucieuse la relation de Chalses
Solution
Utilisation de la relation de Chasles
\(\overrightarrow{ML}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{EL}\)
\(\overrightarrow{ML}=\dfrac{1}{4}\overrightarrow{DA}+\overrightarrow{AE}+\dfrac{1}{4}\overrightarrow{EF}\)
Or ABCDEFGH est un cube donc \(\overrightarrow{AE}=\overrightarrow{DH}\) et \(\overrightarrow{EF}=\overrightarrow{AB}\)
donc \(\overrightarrow{ML}=\dfrac{1}{4}\overrightarrow{DA}+\overrightarrow{DH}+\dfrac{1}{4}\overrightarrow{AB}=\dfrac{1}{4}(\overrightarrow{DA}+\overrightarrow{AB})+\overrightarrow{DH}\)
Donc \(\overrightarrow{ML}=\dfrac{1}{4}\overrightarrow{DB}+\overrightarrow{DH}\)
Question
En déduire la position de la droite (ML) par rapport au plan (DBH).
Solution
\(\overrightarrow{DB}\) et \(\overrightarrow{DH}\) ne sont pas colinéaires donc ils dirigent le plan (DBH)
Le vecteur \(\dfrac{1}{4}\overrightarrow{DB}+\overrightarrow{DH}\) est donc aussi un vecteur du plan (DBH)
Le vecteur \(\overrightarrow{ML}\) est donc aussi un vecteur du plan (DBH)
Mais le vecteur \(\overrightarrow{ML}\) est donc aussi un vecteur directeur de la droite \((ML)\)
Donc d'après les propriétés vues précédemment, la droite \((ML)\) est parallèle au plan \((DBH)\)
On retiendra qu'une droite de vecteur directeur \(\overrightarrow u\) est parallèle au plan \(\mathcal P\) de vecteur directeur \(\overrightarrow v\) et \(\overrightarrow w\) si et seulement si \(\overrightarrow u\) peut se décomposer selon les vecteurs \(\overrightarrow v\) et \(\overrightarrow w\)
c'est à dire qu'il existe deux réels x et y tels que \(\overrightarrow u=x\overrightarrow v+y\overrightarrow w\)
On dit dans ce cas que \(\overrightarrow u\), \(\overrightarrow v\) et \(\overrightarrow w\) sont coplanaires.