ROC : Démonstration du théorème du toit
Vous avez vu en classe de seconde le Théorème du toit. Nous allons en donner une démonstration qui fera l'objet d'une ROC.
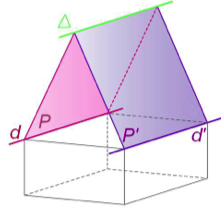
On considère deux droites d et d' sont parallèles telles que :
un plan \(\mathcal P\) contienne la droite d,
un plan \(\mathcal P'\) contienne la droite d',
les plans \(\mathcal P\) et \(\mathcal P'\) sont sécants suivant une droite \(\Delta\),
Question
Soit \(\overrightarrow{w}\) un vecteur directeur de \(\Delta\) et \(\overrightarrow{u}\) un vecteur directeur de \((d)\)
Démontrer que \(\overrightarrow{u}\) et \(\overrightarrow{w}\) sont deux vecteurs de \(\mathcal P\) et \(\mathcal P'\)
Indice
Si une droite \(d\) est incluse dans un plan \(\mathcal P\), tout vecteur directeur de la droite \(d\) est un vecteur du plan \(\mathcal P\) Cela est une conséquence directe de la dernière propriété vue sur cette page.
Solution
\(\Delta \subset \mathcal P\) et \(\overrightarrow w\) dirige \(\Delta\) donc \(\overrightarrow w\) est un vecteur du plan \(\mathcal P\).
\(d \subset \mathcal P\) et \(\overrightarrow u\) dirige \(d\) donc \(\overrightarrow u\) est un vecteur du plan \(\mathcal P\).
\(d//d'\) et \(\overrightarrow u\) est un vecteur directeur de \(d\), donc \(\overrightarrow u\) est aussi un vecteur directeur de \(d'\). Comme ci-dessus, on peut dire que :
\(\Delta \subset \mathcal P'\) et \(\overrightarrow w\) dirige \(\Delta\) donc \(\overrightarrow w\) est un vecteur du plan \(\mathcal P'\)
\((d') \subset \mathcal P'\) et \(\overrightarrow u\) dirige \((d')\) donc \(\overrightarrow u\) est un vecteur du plan \(\mathcal P\)
Conclusion : \(\overrightarrow{u}\) et \(\overrightarrow{w}\) sont deux vecteurs de \(\mathcal P\) et \(\mathcal P'\)
Question
Montrons que \(\overrightarrow{u}\) et \(\overrightarrow{w}\) sont colinéaires.
Indice
On pourra procéder par l'absurde.
Solution
Par l'absurde, supposons que \(\overrightarrow{u}\) et \(\overrightarrow{w}\) ne sont pas colinéaires.
Puisque \(\overrightarrow{u}\) et \(\overrightarrow{w}\) appartiennent à \(\mathcal P\), alors \(\overrightarrow{u}\) et \(\overrightarrow{w}\) dirigent \(\mathcal P\).
Puisque \(\overrightarrow{u}\) et \(\overrightarrow{w}\) appartiennent à \(\mathcal P'\), alors \(\overrightarrow{u}\) et \(\overrightarrow{w}\) dirigent \(\mathcal P'\).
\(\mathcal P\) et \(\mathcal P'\) ont donc même couple de vecteurs directeurs, on en déduit donc d'après les propriétés vues précédemment que \(\mathcal P\) et \(\mathcal P'\) sont parallèles.
Or ceci est contraire aux hypothèses du théorème du toit.
On en déduit donc que \(\overrightarrow{u}\) et \(\overrightarrow{w}\) sont colinéaires.
Question
Conclure que les droites \(d\), \(d'\) et \(\Delta\) sont parallèles.
Solution
Les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{w}\) sont colinéaires.
Par conséquent, \(d\) et \(\Delta\) sont parallèles car elles ont des vecteurs directeurs colinéaires.
Et puisque \(d \slash \hspace{-0.08cm }\slash d'\), on en déduit que \(d\), \(d'\) et \(\Delta\) sont parallèles. cqfd.