Fonction périodique
Définition :
Une fonction \(f\) est périodique de période \(T\) sur \(\mathbb R\) si et seulement si par définition pour tout \(x\in \mathbb R, ~f(x+T)=f(x)\)
Exemple : Sinus et Cosinus
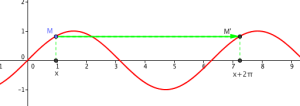
On a vu lors de l'enroulement de la droite sur le cercle trigonométrique qu'ajouter \(2\pi\) à \(x\) revenait à faire un tour complet du cercle trigonométrique. Ainsi les réels \(x\) et \(x+2\pi\) ont même image sur le cercle trigonométrique.
On en déduit ainsi que pour tout \(x\in\mathbb R\), \(\sin (x+2\pi)=\sin x\) et \(\cos (x+2\pi)=\cos x\)
En d'autre termes, les fonctions Sinus et Cosinus sont périodiques de période \(2\pi\).
Complément :
\(4\pi\), \(6\pi\), \(-2\pi\) etc... sont aussi des périodes pour Sinus et Cosinus. Généralement, on considère plutôt la plus petite période positive.
Il est très fréquent de trouver des fonctions périodiques dès lors que l'on travaille avec les fonctions Sinus et Cosinus. Néanmoins la période peut varier en fonction de ce que l'on trouvera à l'intérieur des fonctions Sinus et Cosinus.
Par exemple, la fonction \(f\) qui à tout \(x \in \mathbb R\) associe \(\cos (2x)\) est périodique de période \(\pi\) :
En effet, pour tout \(x\), \(f(x+\pi)=\cos~(2(x+\pi))=\cos~(2x+2\pi)=cos~(2x)=f(x)\)
Remarque : Interprétation graphique
Les fonctions Sinus et Cosinus sont invariantes par translation de vecteur \(2\pi\overrightarrow i\).
