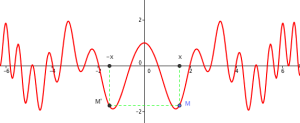
Exemple de parité
On considère \(f : x\longmapsto \cos (2x)-\sin(x^2)\)
Question
Déterminer la parité de \(f\).
Indice
Il s'agit de savoir si la fonction \(f\) est paire, impaire ou rien du tout.
Indice
Dans ce cas, on pourra calculer \(f(-x)\).
Solution
Méthode :
Calculons \(f(-x)=\cos (-2x)-\sin((-x)^2)\)
Or on sait que :
\(\cos(-2x)=\cos (2x)\)
\((-x)^2=x^2\)
Donc \(f(-x)=\cos(2x)-\sin(x^2)=f(x)\)
La fonction \(f\) est donc paire.
Question
Interpréter ce résultat graphiquement.
Solution
La courbe représentative de la fonction \(f\) admet l'axe des ordonnées comme axe de symétrie.
Question
Étudier la dérivabilité de \(f\) et la parité de \(f'\).
Solution
\(f\) est dérivable sur \(\mathbb R\) car les fonctions Sinus et Cosinus le sont ainsi que les fonctions à l'intérieur : \(2x\) et \(x^2\). La composition et la somme de ces fonctions ne pose donc pas de problèmes de dérivabilité.
\(f'(x)=-2\sin(2x)-2x\cos(x^2)\)
\(f'(-x)=-2\sin(-2x)-2(-x-\cos((-x)^2)=2\sin(2x)+2x\cos(x^2)=-f'(x)\)
La fonction \(f'\) est donc \(impaire\).
Ce résultat en réalité peut se généraliser à n'importe quelle fonction paire dérivable.
Question
Soit \(f\) une fonction paire dérivable sur \(\mathbb R\).
Démontrer que \(f'\) est impaire.
Solution
La fonction \(f\) étant paire, on sait que pour tout \(x\in \mathbb R, f(-x)=f(x)\).
Dérivons le membre de gauche de l'égalité : la dérivée de la fonction \(x \longmapsto f(-x)\) vaut \(-f'(-x)\) d'après les propriétés de la dérivation rencontrées précédemment.
Dérivons le membre de droite : on obtient \(f'(x)\).
L'égalité des deux fonctions \(x\longmapsto f(-x)\) et \(x\longmapsto f(x)\) entraîne également l'égalité des dérivées.
On en conclut que \(f'(x)=-f'(-x)\) pour tout \(x\in \mathbb R\) ce qui démontre que la fonction \(f'\) est impaire.