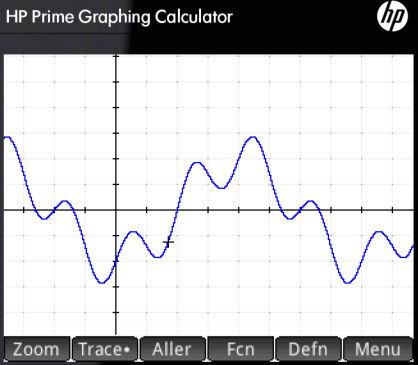
Etude de périodicité
Question
Montrer que la fonction \(f :x\longmapsto \sin ~(2x) -2\cos ~(\dfrac x 2)\) est périodique de période \(4\pi\).
Solution
Pour tout \(x\in\mathbb R\) \(f(x+4\pi)=\sin \left(2(x+4\pi)\right)-2\cos\left(\dfrac{x+4\pi}{2}\right)\).
Or, \(\cos\left(\dfrac{x+4\pi}{2}\right)=\cos\left(\dfrac{x}{2}+\dfrac{4\pi}{2}\right)=\cos\left(\dfrac{x}{2}+2\pi\right)=\cos\left(\dfrac{x}{2}\right)\) car on sait que la fonction Cosinus est périodique de période \(2\pi\).
De plus \(\sin \left(2(x+4\pi)\right)=\sin(2x+8\pi)=\sin(2x+2\pi+2\pi+2\pi+2\pi)=\sin(2x)\) car on sait que la fonction Sinus est périodique de période \(2\pi\).
Ainsi, \(f(x+4\pi)=\sin (2x) -2\cos (x/2) =f(x)\).
La fonction \(f\) est donc périodique de période \(4\pi\).