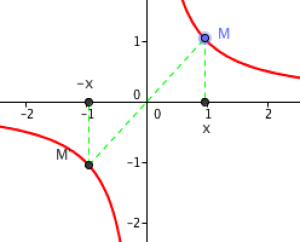
Fonctions impaires
Définition :
Une fonction est impaire si et seulement si pour tout \(x\in\mathcal D_f, ~-x \in \mathcal D_f ~\text {et}~ f(-x)=-f(x)\).
Complément : Interprétation géométrique
La courbe représentative d'une fonction impaire est symétrique par rapport à l'origine du repère.
Exemple : La fonction inverse
La fonction \(x\longmapsto \dfrac{1}{x}\) est une fonction impaire.
En effet, pour tout \(x\in\mathbb R-{0},~ \dfrac{1}{-x}=-\dfrac{1}{x}\).
Les deux branches d'hyperbole représentant la fonction inverse sont symétriques par rapport à l'origine du repère.