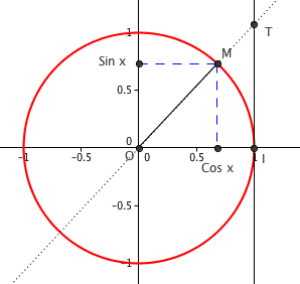
Dérivabilité en 0
On cherche dans cette activité à déterminer les nombres dérivés des fonctions Sin et Cos en utilisant uniquement des propriétés géométriques et les définitions de base du cours.
Construction de la figure
Question
Montrer que \(IT=\dfrac{\sin x}{\cos x}\).
Indice
On pourra penser au théorème de Thalès.
Solution
Les droites (MC) et (IT) sont parallèles, donc les triangles OMC et OTI sont dans une configuration de Thalès. On a donc :
\(\dfrac{OC}{OI}=\dfrac{MC}{TI}\).
Or, \(OC=\cos x\), \(OI=1\) et \(MC=\sin x\). On en déduit donc :
\(\dfrac{\cos x}{1}=\dfrac{\sin x}{TI}\) donc par produit en croix :
\(IT=\dfrac{\sin x}{\cos x}\)
Question
En rangeant par ordre croissant les aires des triangles \(OIM\), \(OIT\) et l'aire du secteur de disque \(OIM\), montrer que pour tout \(x\in \left]0 ;\dfrac{\pi}{2}\right[\), \(\sin x\leqslant x\leqslant \dfrac{\sin x}{\cos x}\).
Indice
On pourra remarquer que l'aire d'un secteur de disque de rayon \(r\) et d'angle de mesure \(\alpha\) exprimée en radian, est égale à \(\dfrac{\alpha}{2}\times r^2\) par principe de proportionnalité de l'aire par rapport à la longueur de l'arc.
Solution
Aire du triangle OIM
Le triangle OIM a pour base OI et hauteur MC donc son aire vaut :
\(\mathcal {A}_{OIM}=\dfrac{1\times \sin x}{2}=\dfrac{\sin x}{2}\)
Aire du triangle OIT
Le triangle OIT a pour base OI et hauteur IT donc son aire vaut :
\(\mathcal {A}_{OIT}=\dfrac{1\times \dfrac{\sin x}{\cos x}}{2}=\dfrac{\sin x}{2\times \cos x}\)
Aire du secteur de disque OIM
L'angle \(\alpha\) exprimé en radian vaut \(x\) et le rayon du disque vaut 1 donc l'aire du secteur de disque vaut \(\mathcal A_D=\dfrac{x}{2}\).
Nous remarquons que \(\mathcal {A}_{OIM}\leqslant \mathcal {A}_{D}\leqslant \mathcal {A}_{OIT}\)
Donc \(\dfrac{\sin x}{2}\leqslant \dfrac{x}{2}\leqslant \dfrac{\sin x}{2\times \cos x}\)
En multipliant par deux, on obtient donc l'inégalité demandée :
pour tout \(x\in \left]0 ;\dfrac{\pi}{2}\right[\), \(\sin x\leqslant x\leqslant \dfrac{\sin x}{\cos x}\)
Question
En déduire que pour tout \(x\in \left]0 ;\dfrac{\pi}{2}\right[\), \( \cos x\leqslant \dfrac{\sin x}{x} \leqslant 1\).
Indice
On se rappellera que la fonction inverse est strictement décroissante sur \(]0 ;+\infty[\)
Solution
On a montré que pour tout \(x\in \left]0 ;\dfrac{\pi}{2}\right[\), \(\sin x\leqslant x\leqslant \dfrac{\sin x}{\cos x}\).
Or si \(x\in \left]0 ;\dfrac{\pi}{2}\right[\), on sait que \(\sin x>0\) et \(\cos x>0\) Donc on peut prendre l'inverse de l'inégalité démontrée en renversant les sens des inégalités puisque la fonction inverse est strictement décroissante sur \(]0 ;+\infty[\):
\(\dfrac{1}{\sin x}\geqslant \dfrac{1}{x}\geqslant \dfrac{\cos x}{\sin x}\)
Multiplions à présent cette inégalité par \(\sin x\) dont on sait qu'il est positif pour \(x\in \left]0 ;\dfrac{\pi}{2}\right[\). On obtient :
\(\dfrac{\sin x}{\sin x}\geqslant \dfrac{\sin x}{x}\geqslant \dfrac{\sin x \times \cos x}{\sin x}\) et donc en simplifiant par \(\sin x\neq 0\) on obtient :
pour tout \(x\in \left]0 ;\dfrac{\pi}{2}\right[\), \( \cos x\leqslant \dfrac{\sin x}{x} \leqslant 1\).
On montre de manière analogue que cette inégalité reste vraie pour tout \(x\in \left]-\dfrac{\pi}{2} ;0\right[\)
Question
En déduire que la fonction \(f :x\longmapsto \sin(x)\) est dérivable en 0. Donner \(f'(0)\).
Indice
On se rappellera la définition du nombre dérivé en un point.
Solution
Par définition du nombre dérivé, On sait que \(f'(0)=\lim\limits_{h\to0} \dfrac{f(0+h)-f(0)}{h}\) si cette limite existe.
Or \(\dfrac{f(0+h)-f(0)}{h}=\dfrac{\sin h}{h}\) qui est une forme indéterminée en 0.
Mais on vient de montrer que \( \cos x\leqslant \dfrac{\sin x}{x} \leqslant 1\) pour \(x\in \left]-\dfrac{\pi}{2} ;\dfrac{\pi}{2}\right[ -\{0\}\).
De plus :
\(\lim\limits_{h\to 0}~\cos (h)=\cos(0)=1\)
\(\lim\limits_{h\to0} 1=1\)
Donc d'après le théorème des gendarmes, on en déduit que \(\lim\limits_{h\to0} \dfrac{f(0+h)-f(0)}{h}=\lim\limits_{h\to0} \dfrac{sin(0+h)-sin(0)}{h}=\lim\limits_{h\to0} \dfrac{sin(h)}{h}=1\).
Ce qui montre l'existence de \(f'(0)\) et sa valeur.
Question
Montrer que pour tout réel \(h\in \left]-\dfrac{\pi}{2} ;\dfrac{\pi}{2}\right[ -\{0\}\), on a :
\(\dfrac{\cos h-1}{h}=\dfrac{\sin h}{h}\times \dfrac{-\sin h}{\cos h+1}\)
Indice
On pourra multiplier et diviser par \(\cos h+1\) et utiliser la relation fondamentale de la trigonométrie.
Solution
Si \(h\in \left]-\dfrac{\pi}{2} ;\dfrac{\pi}{2}\right[ -\{0\}\), alors \(\cos h+1\neq 0\). On peut donc écrire que :
\(\dfrac{\cos h-1}{h}=\dfrac{\cos h-1}{h}\times \dfrac{\cos h+1}{\cos h+1}\)
Or \((\cos h-1)\times (\cos h+1)=\cos^2 h - 1=-\sin^2 h\) puisque \(\cos^2h+\sin^2 h=1\)
Donc \(\dfrac{\cos ~h-1}{h}=\dfrac{-\sin^2h}{h(\cos ~h+1)}=\dfrac{\sin ~h}{h}\times \dfrac{-\sin~ h}{\cos ~h+1}\)
Question
En déduire le nombre dérivé de la fonction cosinus en 0.
Solution
On sait que :
\(\lim\limits_{h\to0} \dfrac{\sin ~h}{h}=1\)
\(\lim\limits_{h\to0}~ \dfrac{-\sin ~h}{\cos~ h+1}=\dfrac{ 0}{1}=0\)
Et puisque :
pour tout réel \(h\in \left]-\dfrac{\pi}{2} ;\dfrac{\pi}{2}\right[ -\{0\}\), on a \(\dfrac{\cos h-1}{h}=\dfrac{\sin h}{h}\times \dfrac{-\sin h}{\cos h+1}\)
On en déduit par opération sur les limites que \(\cos' 0=\lim\limits_{h\to0} \dfrac{\cos h-\cos 0}{h}=0\times 1=0\)