Soit \(f\) la fonction définie sur \(I=[0 ;2\pi]\) par \(f :x\longmapsto \sin x+\cos x\)
Question
Justifier que \(f\) est dérivable sur et calculer \(f'\).
Solution
Les fonctions Sinus et Cosinus sont dérivables sur \(\mathbb R\) donc la somme de ces deux fonctions est aussi dérivable sur \(\mathbb R\).
On a \(f'(x)=\cos x-\sin x\)
Question
En étudiant les positions relatives de Cosinus et Sinus, préciser le signe de \(f'\) sur I puis dresser le tableau de variations de la fonction \(f\) sur \(I\).
Solution
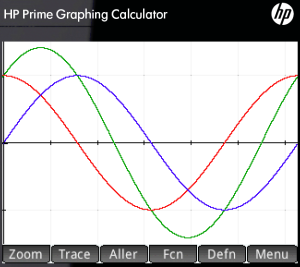
Étudier le signe de \(f'(x)=\cos x-\sin x\) revient à étudier la position relative des courbes représentant les fonctions Sinus et Cosinus. Observons le tracé de ces deux courbes sur la calculatrice :
Méthode : Résoudre l'équation Sin x= Cos x
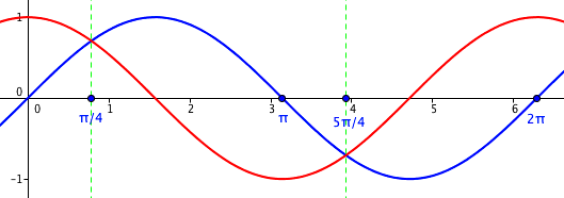
L'observation du graphique montre qu'il nous faut déterminer les deux valeurs pour lesquelles \(\sin x=\cos x\) sur l'intervalle \([0 ;2\pi]\).
Si l'on se rappelle la définition géométrique de Cosinus et Sinus, les valeurs de \(x\) recherchées sont celles pour lesquelles l'abscisse et l'ordonnée du point M sont égales. Il nous faut donc déterminer les deux points d'intersection du cercle trigonométrique avec la droite d'équation \(y=x\).
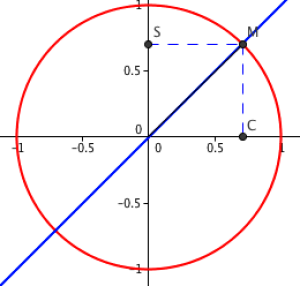
La première correspond à la valeur remarquable \(x=\dfrac{\pi}{4}\) dont on sait que le Sinus et le Cosinus valent tous deux \(\dfrac{\sqrt 2}{2}\).
La seconde correspond à la valeur remarquable \(x=\pi+\dfrac{\pi}{4}=\dfrac{5\pi}{4}\) dont on sait que le Sinus et le Cosinus valent tous deux \(-\dfrac{\sqrt 2}{2}\).
Ainsi, en observant les courbes représentatives de Sinus et Cosinus, on obtient :
Si \(x\in \left[0 ;\dfrac{\pi}{4}\right[\cup\left]\dfrac{5\pi}{4} ;2\pi\right], \cos x>\sin x\) donc \(f'(x)>0\)
Si \(x\in \left]\dfrac{\pi}{4} ;\dfrac{5\pi}{4}\right[, \cos x<\sin x\) donc \(f'(x)<0\)
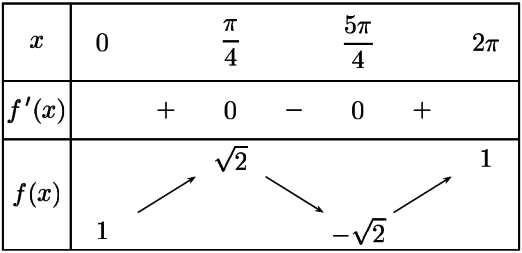
On en déduit le tableau de variations suivant pour la fonction f sur l'intervalle \([0 ;2\pi]\)
On vérifie à l'aide de la calculatrice la représentation graphique de la fonction f sur l'intervalle \([0 ;2\pi]\).