Le calcul de l'impôt
Extrait de la "fiche de calculs facultatifs". Impôt sur les revenus 2011
Voici un extrait de la fiche de calcul pour les impôts 2011.

Dans toute cette activité, on considérera le revenu d'un célibataire. Le nombre N de parts est alors égal à 1.
Question
Un célibataire a un revenu imposable annuel de 6000 €. Calculer son impôt. Comment interpréter ce résultat ?
Même question avec un revenu imposable de 20000 €.
Solution
Pour un revenu annuel de 6000 €
On applique la formule correspondant à la tranche de 5963€ - 11896€ : \(R\times 0,055-327,97\times N\) avec \(R=6000\) et \(N=1\) ce qui donne un impôt de 2,03 € !
Rien de bien étonnant à cela, 6000 étant juste au dessus du seuil où l'on commence à payer. Pour une certaine équité, il faut assurer une continuité au niveau des barèmes afin de ne pas avoir de saut pour quelques euros gagnés en plus par an.
Pour un revenu annuel de 20000 €
On applique la formule correspondant à la tranche de 11896€ - 26420€ : \(R\times 0,14-1339,13\times N\) avec \(R=20000\) et \(N=1\) ce qui donne un impôt de 1460,87 € !
Question
Une personne a un revenu imposable de 20000€. Vérifier que son impôt se décompose de la manière suivante :
Rien sur les 5963 premiers euros,
5,5% sur les 5933 euros restants,
14% sur le reste de ses revenus.
Solution
20000=5963+5933+8104
5933*0,055=326,31
8104*0,14=1134.56
0+326,31+1134,56=1460,88
On retrouve ainsi par cette décomposition des revenus en tranches la somme exacte trouvée dans la question précédente en utilisant la formule donnée par les impôts. Cela nous éclaire donc sur la notion de tranches d'imposition. Le taux d'imposition de la tranche n'est appliqué que sur la part des revenus présents dans la tranche et non la totalité !
Question
Une personne a un revenu imposable de 30000 €. Donner la décomposition de son impôt selon les tranches d'imposition comme à la question précédente.
Solution
Les 30000 € se répartissent ainsi :
0% pour les 5963 premiers euros,
5,5% pour les 5933 euros suivants,
14% pour les 14524 euros suivants,
30% pour les 3580 euros restants.
Question
Une personne célibataire dont le revenu est 11000 € vous tient cette conversation :
« Heureusement que je n'ai pas fait d'heures supplémentaires, car alors j'aurai changé de tranche et mon taux d'imposition aurait presque triplé. J'aurai perdu de l'argent dans l'opération. »
Que lui répondez-vous ?
Solution
Bien sur que non ! L'impôt est progressif. La tranche d'imposition supérieure n'aurait été appliquée que sur la partie qui dépasse le seuil de la tranche et non sur la totalité de la somme gagnée.
Question
On note \(f :x \longmapsto f(x)\) la fonction qui donne l'impôt d'une personne célibataire ayant un revenu imposable de \(x\) €.
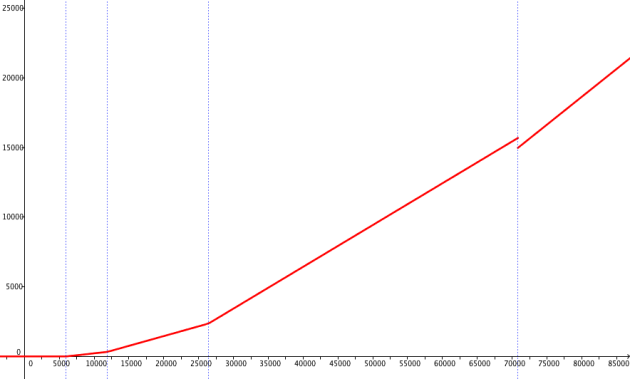
Représenter dans un repère dont l'unité est 1cm pour 2500€ la courbe représentative de \(f\).
Quelles conclusions pouvez-vous tirer à l'observation de ce graphique ?
Solution
Remarque :
On observe sur les 4 premières tranches une parfaite continuité de la courbe ce qui traduit la progressivité de l'impôt dont on a parlé aux questions précédentes.
Néanmoins sur la dernière tranche, une discontinuité apparaît à la hauteur de 70830 €. Cela traduit une anomalie sur le document officiel des impôts : il est en effet injuste qu'une personne gagnant 70831 €/an paye moins d’impôts qu'une personne touchant 70829 €/an !
Question
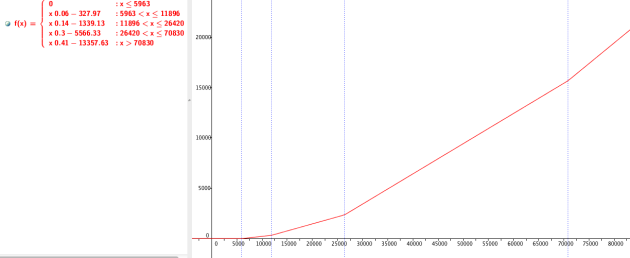
Corriger le document des impôts afin de donner la bonne formule sur la dernière tranche d’imposition.
Solution
Une manière de corriger la courbe est de remplacer le taux de 0,4 dans la formule par 0,41 : la dernière tranche étant à 41% et non 40% comme le laisse penser l'entête de l'extrait du document des impôts. En utilisant la formule \(R\times 0,41-13357,63\times N\), la courbe devient de nouveau continue sur l'ensemble des revenus.