Limite infinie
Définition :
On dit que la suite \((u_n)\) admet pour limite \(+\infty\) si tout intervalle de la forme \(]A ;+\infty[\) (où A est un réel) contient tous les termes \(u_n\) de la suite à partir d'un certain rang, autrement dit, si, quelque soit le nombre A, les termes de la suite\((u_n)\) dépasse A à partir d'un certain rang.
On dit que la suite \((u_n)\) admet pour limite \(-\infty\) si tout intervalle de la forme \(]-\infty ;B[\) (où B est un réel) contient tous les termes \(u_n\) de la suite à partir d'un certain rang. Cela revient à dire que \((-u_n)\) tend vers \(+\infty\).
On note alors \(\lim\limits_{n \to +\infty} u_n=+\infty\) (respectivement \(\lim\limits_{n \to +\infty} u_n=-\infty\)).
Exemple :
La suite \((u_n)\) définie sur \(\mathbb N\) par \(u_n=n^2\) a pour limite \(+\infty\).
En effet, soit A un réel positif, l'intervalle \(]A ;+\infty[\) contient tous les termes de la suite dès lors que \(n>\sqrt A\) (puisque la fonction carré est croissante sur \(\mathbb R^+\)).
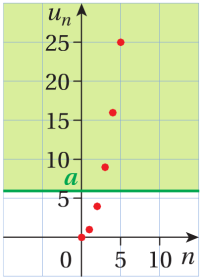
Exemple :
La suite \((v_n)\) définie sur \(\mathbb N\) par \(v_n=-\sqrt n\) a pour limite \(-\infty\).
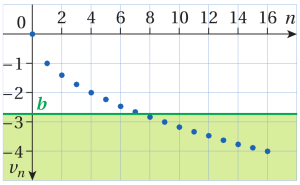
En effet soit B un réel négatif.
\(-\sqrt n < B \Longleftrightarrow n > B^2\) en élevant au carré. En effet la fonction carré est décroissante sur \(\mathbb R^-\)
Par conséquent, tous les termes \(v_n\) de rang supérieur à \(B^2\), seront dans l'intervalle \(]-\infty ;B[\).