Soit la suite \((v_n)\) définie pour tout \(n\) par par \(v_n=3-n^2\).

Question

A l'aide de la calculatrice, conjecturer qu'il existe un rang N au delà duquel \(v_n<-1000\).

Quel est ce rang ?

Solution

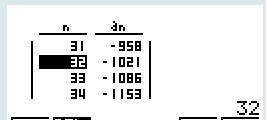
Il semble que pour \(n\geqslant 32\), les valeurs de la suite \((u_n)\)descendent en dessous du seuil de -1000.

Question

Démontrer par le calcul la conjecture de la question précédente.

Solution

\(3-n^2<-1000 \Longleftrightarrow -n^2<-1003 \Longleftrightarrow n^2>1003\Longleftrightarrow n>\sqrt{1003}\approx 31,7\)

(on renverse l'inégalité par passage à l'opposé pour la 1ère équivalence et on la

conserve pour la 2èmecar la fonction racine est croissante sur \(\mathbb R^+\)).

Par conséquent, à partir d'un rang n supérieur à 32, tous les termes de la suite \((v_n)\) sont dans l'intervalle \(]-\infty ;-1000[\).

Question

Généraliser le résultat de la question précédente à n'importe quel seuil B.

Montrer ainsi que \((v_n)\) est divergente et que sa limite est \(-\infty\)

Solution

Soit un réel B négatif.

\(3-n^2<B \Longleftrightarrow -n^2<B-3\)

\(3-n^2<B \Longleftrightarrow n^2>3-B\) (on renverse l'inégalité par passage à l'opposé)

\(3-n^2<B \Longleftrightarrow n>\sqrt{3-B}\) (si B<0, 3-B est positif et la fonction racine est croissante sur \(\mathbb R^+\))

Par conséquent, à partir d'un rang n supérieur à \(\sqrt{3-B}\), tous les termes de la suite \((v_n)\) sont dans l'intervalle \(]-\infty ;B[\)

Question

On considère l'algorithme suivant :

1
Initialisation
2
... Saisir B
3
... N prend la valeur 0
4
... V prend la valeur 3
5
Traitement
6
... Tant que V>B Faire
7
... ... N prend la valeur N+1
8
... ... V prend la valeur 3-N^2
9
... Fin Tant que
10
Sortie
11
... Afficher N

Cet algorithme s'arrête t-il à un moment ? Justifier.

Solution

On sait que la suite \((v_n)\) tend vers \(-\infty\). Quelle que soit la valeur de B saisie, on sait qu'à partir d'un certain rang N, les valeurs v_N seront inférieures à B, ce qui mettra fin à la boucle Tant que. L'algorithme s’arrête donc en affichant la plus petite valeur de n où le seuil B est dépassé.

Question

Programmer l'algorithme ci-dessus sur Python ou votre calculatrice et donner la valeur retournée par celui-ci. lorsqu'on saisit la valeur -100.

Ce résultat est-il cohérent avec le travail fait dans la première question ?

Solution

Voici le lien vers le programme réalisé en Python. Le code du programme est écrit ci-dessous.

1
# Initialisation
2
B=int(input("Saisir une valeur pour B"))
3
N=0
4
V=3
5
# Traitement
6
while V>B:
7
   N=N+1
8
   V=3-N**2
9
# Sortie
10
print(N)

La valeur retournée pour \(B=-100\) est \(N=11\).

Nous avions déterminé en première question que lorsque \(n>\sqrt{3-B}\), alors \(v_n<B\).

Or \(\sqrt{3-B}=\sqrt{103}\approx 10,15\) donc pour \(n\geq11\), le seuil de -100 est dépassé, ce qui est bien le résultat donné par le programme.