Introduction de la notion de limite finie

On considère la suite \((u_n)\) définie par \(u_0=10\) et \(u_{n+1}=\frac{3}{5}u_n+2\).

Question

En utilisant une calculatrice ou un ordinateur, donner des valeurs approchées de \(u_1\) à \(u_{10}\) puis des valeurs approchées de \(u_{20}\) et de \(u_{50}\) .

Émettre une conjecture sur la valeur limite de la suite \((u_n)\)

Solution

Question

Soit h un réel strictement positif.

Montrer que si \(5-h<u_n<5+h\), alors \(5-h<u_{n+1}<5+h\)

Solution

Question

Démontrer par récurrence que pour tout \(n\geqslant 8\) on a \(4,9 \leqslant u_n\leqslant 5,1\)

Solution

Question

Déterminer un entier N tel que pour tout \(n\geqslant N\) on ait \(4,999 \leqslant u_n \leqslant 5,001\)

Solution

Importance de l'initialisation !

Nous avons démontré que

  • pour un nombre h donné si il existe un rang \(n_0\) tel que \(5-h<u_{n_0}<5+h\) alors pour tout entier \(n\geqslant n_0\) il en sera de même.

  • pour \(h=0,1\), le tableau de valeurs de la calculatrice nous donne l’existence d'un tel \(n_0\) (8)

  • pour \(h=0,001\), il suffit de prendre \(n_0=20\)

Par contre rien ne nous assure que pour n'importe quelle valeur de \(h>0\), un tel rang \(n_0\) existe !

On peut toutefois conjecturer l'existence d'un tel rang \(n_0\) pour n'importe quelle valeur de \(h>0\) au moyen d'un algorithme, comme le suggère la question suivante :

Question

Écrire un algorithme prenant en entrée un nombre \(h>0\) et retournant le plus petit entier \(n_0\) tel que \(5-h<u_{n_0}<5+h\)

Programmer cet algorithme sur la calculatrice pour en déduire à partir de quel rang les termes de la suite \((u_n)\) seront à une distance inférieure à 0,000001 de la limite \(\ell=5\)

Solution

1
Entrées
2
... n=0
3
 ... U=10
4
... h prend la valeur 0
5
... Tant que h<=0 faire
6
 ... ... Saisir h
7
... Fin tant que
8
Traitement
9
... Tant que abs(U-5)>h Faire
10
... ... n prend la valeur n+1
11
... ... U prend la valeur 3/5*U+2
12
... Fin Tant que
13
Sortie
14
... Afficher n
Complément

Dans cet algorithme, une boucle « Tant que » a été introduite dans la partie entrée pour demander à l'utilisateur de saisir une valeur pour h tant qu'il s'obstine à rentrer une valeur négative ou nulle. Cela protège le programme l’empêchant de tourner indéfiniment si la valeur entrée n'est pas strictement positive.

ComplémentValeur absolue

Une astuce a été utilisée dans la condition en utilisant la fonction Valeur absolue.

Cette fonction \(x\longmapsto abs(x)\) renvoie

  • x si x est positif

  • -x si x est négatif

Ainsi \(abs(-5)=5\) et \(abs(3)=3\)

La condition \(abs(U-5)>h\) revient à dire que la distance entre U et 5 est supérieure à h donc \(U<5-h\) ou \(U>5+h\)

SimulationProgramme Casio

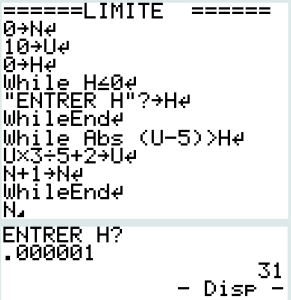
Voici le programme correspondant sur Casio. La valeur absolue se trouve dans \(\fbox{OPTN}\) \(\fbox {NUM}\). Ceux qui préfère saisir \(U<5-h\) ou \(U>5+h\) trouveront les relations logiques dans \(\fbox{OPTN}\) \(\fbox {LOGIC}\)

Pour démontrer rigoureusement l'existence d'un tel rang \(n_0\) pour n'importe quelle valeur de \(h>0\), une démonstration mathématique s'impose. Une possibilité est de passer par nos connaissances sur les suites géométriques.

Question

Soit \((v_n)\) la suite définie pour tout entier naturel n par \(v_n=u_n-5\)

Démontrer que \((v_n)\) est géométrique et préciser sa raison.

En déduite la limite de \((v_n)\)

Solution

Montrons que (vn) est géométrique

\(v_{n+1}=u_{n+1}-5=\dfrac{3}{5}u_n+2-5=\dfrac{3}{5}u_n-3=\dfrac{3}{5}\left(u_n-5\right)=\dfrac{3}{5}v_n\)

Donc la suite \((v_n)\) est géométrique de raison \(\dfrac{3}{5}\)

ComplémentEn déduire sa limite.

On sait depuis la classe de première que la limite des suites géométriques de raison \(0<q<1\) est 0.

Donc \(\lim\limits_{n \to +\infty} v_n=0\)

Question

En déduire la limite de \((u_n)\)

Solution

Puisque \(u_n=v_n+5\), et puisque \((v_n)\) tend vers 0, on en déduit bien que \((u_n)\) tend vers \(0+5=5\)