Calculer une espérance
Lors d'un test de connaissances, 70% des individus ont un score inférieur à 60 points.
De plus, les résultats suivent une loi normale d'écart-type 20.
Question
Calculer l'espérance de cette loi.
Indice
On pourra essayer de se ramener à une loi centrée réduite en posant \(Z=\dfrac{X-\mu}{\sigma}\)
Indice
On sait que \(\mathbb P(X\leqslant 60)=0,70\).
Indice
On utilisera la fonction Inverse Normal de la calculatrice pour trouver le nombre s tel que \(\mathbb P(Z\leqslant s)=0,70\).
Solution
Posons \(Z=\dfrac{X-\mu}{\sigma}\). \(~~Z\hookrightarrow \mathcal N(0 ;1)\)
On sait que \(\mathbb P(X\leqslant 60)=0,70\).
Ramenons-nous à la loi centrée réduite et cherchons le nombre \(s\) tel que \(\mathbb P(Z\leqslant s)=0,70\)
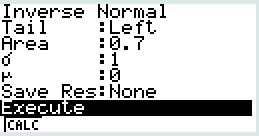
Cela se fait en utilisant la fonction inverse normal sur Casio. On place Tail à Left car Z est à gauche de la borne s cherchée. La réponse obtenue est 0,524.
Sur TI, on va utiliser la fonction invNorm( de la manière suivante :
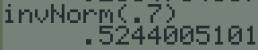
On sait par le passage à la loi réduite que \(\dfrac{60-\mu}{20}=s\)
Une fois la valeur de \(s\approx 0,524\) trouvée, on en déduit l'espérance par une simple équation :
\(\mu\approx 60-20\times 0.524\approx 49,5\)