Soit \(X\) une v.a continue qui suit une loi normale \(\mathcal N(10 ;0,8^2)\). Déterminer une valeur approchée de \(t\) au centième telle que :
\(P(X\leq t)=0,95\)
\(P(X\geq t)=0,85\)
On utilise la fonction loi normale inverse de la calculatrice.
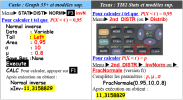
Pour déterminer \(t\) tel que : \(P(x\leq t)=0,95\) on utilise les instructions suivantes :
Pour déterminer \(t\) tel que : \(P(x\geq t)=0,85\) :
sur Casio : on remplace "left" par "right" : on trouve \(t\approx9,17\).
Sur TI, il faut procéder auparavant à une petite transformation :
\(P(X< t)=1-P(X> t)=1-0,85=0,15\)
Puis on applique la méthode précédente. On trouve \(t\approx9,17\).
