Les températures du mois de juillet autour du lac Léman suivent la loi normale d'espérance 18,2°C et d'écart type 3,6°C.
Une personne part camper en juillet sur le pourtour du lac.
Question
Calculer la probabilité que la température :
soit inférieure à 16°C
soit comprise entre 20°C et 24,5°C
soit supérieure à 21°C
Solution
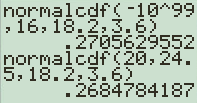
Soit \(X\hookrightarrow \mathcal N(18,2;3,6^2)\)
\(\mathbb P(x\leqslant 16)\approx 0,27\)
\(\mathbb P(20\leqslant x\leqslant 24,5)\approx 0,27\)
\(\mathbb P(x\leqslant 16)\approx 0,268\)
\(\mathbb P(x\geqslant 21)\approx 0.218\)

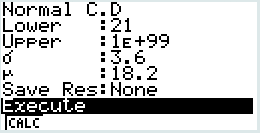
Attention :
Dans l'écriture de la loi normale : \(X\hookrightarrow \mathcal N(18,2;3,6^2)\), on fait apparaître la variance.
Dans l'usage des fonctions de la calculatrice, c'est bien l'écart type qui est à renseigner.
Méthode : Intervalles non bornés
Pour simplifier le calcul sur un intervalle non borné (\(]-\infty ;b]\) ou \([a ;+\infty[\)), une astuce consiste à mettre \(10^{99}\) (ou \(-10^{99}\)) en lieu et place de la borne infinie.