Tableau de variation
Définition : Fonction croissante - Fonction décroissante : approche intuitive.
On dira qu'une fonction f est croissante sur un intervalle \(I=[a ;b]\) si, lorsque x augmente de a vers b, les valeurs de \(f(x)\) augmentent également.
On dira qu'une fonction f est décroissante sur un intervalle \(I=[a ;b]\) si, lorsque x augmente de a vers b, les valeurs de \(f(x)\) diminuent.
Pour synthétiser les variations d'une fonction, on a recours à un tableau de variation. Dans ce tableau, on indique le comportement de la fonction sur chaque intervalle intéressant et les valeurs de la fonction aux points intéressants.
Méthode :
Soit f une fonction définie sur un intervalle D. Pour construire le tableau de variations de la fonction f
on détermine les intervalles I dans D pour lesquels f est monotone, c'est à dire soit croissante, soit décroissante,
on note les résultats obtenus dans un tableau où des flèches indiquent la croissance ou la décroissance de f,
on fait apparaître au bout des flèches les images de la fonction aux bornes des intervalles I considérés.
Exemple :
Dans l'activité de la fourmi paresseuse, l'évolution de la longueur du trajet en fonction de la longueur \(NB~'\) peut être résumée dans le tableau suivant.
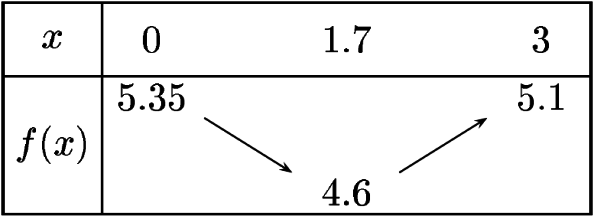
On voit ainsi que la longueur du trajet décroît sur l'intervalle \([0;1,7]\) puis croît sur l'intervalle \([1,7;3]\).
Le tableau fait ainsi apparaître clairement une valeur qui est le trajet minimum que peut parcourir la fourmi.