Activité :La fourmi paresseuse
Une fourmi alléchée par l'odeur du sucre mais paresseuse se demande quel est le chemin le plus court pour atteindre l'objet de sa convoitise.
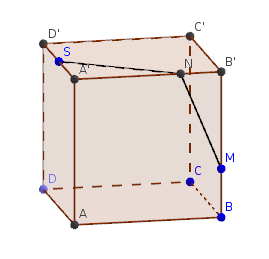
Sur la figure ci-contre, le point M désigne la fourmi et le point S, le morceau de sucre.
On cherche la position du point N sur l’arête [A'B'] tel que le trajet M-N-S soit le plus court possible
On donne les longueurs suivantes :
Le cube a pour coté 3cm
BM=1
S est le milieu de [A'D']
Question
Dans un premier temps, on suppose que la fourmi passe par B'.
Déterminer la longueur du trajet.
Solution
Le trajet M-N-S s'obtient par la somme MB'+B'S.
MB'=2cm
Appliquons Pythagore dans le triangle rectangle SA'B' :
\(SA'^2+A'B'^2=SB'^2\)
\(donc B'S=\sqrt{1,5^2+3^2}=\sqrt{11,25}\approx 3.35\)
La fourmi parcourt donc environ 5,35cm
Question
Dans un premier temps, on suppose que la fourmi passe par N tel que B'N=1cm.
Déterminer la longueur du trajet.
Solution
Le trajet M-N-S s'obtient par la somme MB'+B'S.
Appliquons Pythagore dans le triangle rectangle MNB' :
\(MB'^2+NB'^2=MN^2\)
\(donc MN=\sqrt{2^2+1^2}=\sqrt{5}\approx 2,23\)
Appliquons Pythagore dans le triangle rectangle SA'N :
\(SA'^2+A'N^2=SN^2\)
\(donc NS=\sqrt{1,5^2+2^2}=\sqrt{6,25}\approx 2.5\)
La fourmi parcourt donc environ 4.73cm.
Ce dernier trajet est plus court que celui passant par B'
Nous avons donc mis en évidence que la longueur du trajet varie en fonction de la position du point N.
Il nous faut maintenant déterminer le plus court chemin. Nous allons pour cela introduire la fonction \(f(x)\) qui donne la longueur du trajet M-N-S en fonction de la variable \(x=NB~'\)
Question
Exprimer \(f(x)\) en fonction de \(x\)
Solution
On applique la même méthode que la question précédente en remplaçant 1 par \(x\) dans les calculs.
Appliquons Pythagore dans le triangle rectangle MNB' :
\(MB'^2+NB'^2=MN^2\)
\(donc MN=\sqrt{2^2+x^2}=\sqrt{4+x^2}\)
Appliquons Pythagore dans le triangle rectangle SA'N :
\(SA'^2+A'N^2=SN^2\)
\(donc NS=\sqrt{1,5^2+(3-x)^2}=\sqrt{2,25+(3-x)^2}\)
La fourmi parcourt donc \(f(x)=\sqrt{4+x^2}+\sqrt{2,25+(3-x)^2}\)
On ne cherchera pas à donner une forme simplifiée de f(x). La détermination du chemin le plus court se fera par lecture graphique de la courbe représentant la fonction \(f\).
Question
Sur quel intervalle la fonction f est elle définie ?
Solution
Pour notre problème, la variable x est une longueur comprise entre 0 et 3. Donc \(\mathcal D_f=[0 ;3]\)
Question
Tracer sur la calculatrice la courbe représentative de la fonction \(f\).
Décrire la manière dont cette fonction varie lorsque x augmente.
Solution
Méthode : Tracer la fonction
On introduit tout d'abord la fonction dans la calculatrice : 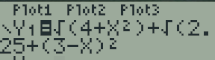
On doit ensuite régler l'échelle de la fenêtre graphique. Pur cela on s'aide des deux indices suivants :
L'ensemble de définition de la fonction nous donne les réglages pour X
Pour Y, on a les deux valeurs calculées à la main au début de l'activité qui nous donne une idée de la grandeur pour.
Voici ci-contre des réglages donnant une bonne idée de la courbe
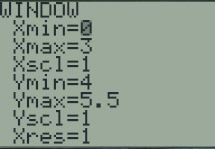
Il ne reste plus qu'à tracer la courbe.
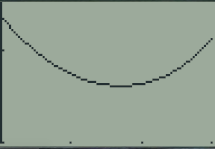
Variations de la fonction
Lorsque x part de 0 et augmente jusqu'à 3, on lit sur la courbe que
Dans un premier temps, la longueur du trajet diminue au fur a mesure que x augmente
Ensuite, passé une certaine valeur de x autour de 1,7, la longueur du trajet se met de nouveau à augmenter.
Ces variations de f(x) mettent en évidence la présence d'une valeur de x pour laquelle le trajet est le plus court. C'est la solution à notre problème.
Question
A l'aide du mode \(\fbox{TRACE}\) de la calculatrice, déterminer une valeur approchée de la valeur de x permettant de réaliser le trajet le plus court. Quelle est alors la longueur de ce trajet minimal ?
Solution
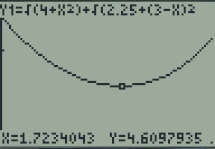
Le trajet le plus court est quand la fourmi passe par le point N situé à environ 1,7cm du point B'
La longueur totale de ce trajet est alors d'environ 4,6 cm
On vérifie bien que ces résultats sont cohérents avec ceux obtenus par les deux premiers calculs.
L'étude des variations d'une fonction nous permet donc de connaître l'évolution d'un phénomène et de solutionner bon nombre de problèmes de la vie courante.