Fonctions décroissantes
Définition : Définition rigoureuse d'une fonction décroissante
Une fonction f est décroissante sur un intervalle I lorsqu'elle inverse l'ordre des nombres sur cet intervalle.
Autrement dit, quelque soient les réels \(a\) et \(b\) appartenant à I, si \(a<b\) alors \(f(a)\geq f(b)\).
Complément : Interprétation graphique
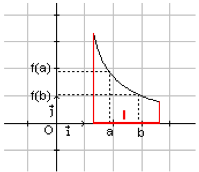
La fonction f est décroissante sur I car sur cet intervalle, la courbe "descend" quand on la lit de la gauche vers la droite.
Lorsque les valeurs de \(x\) augmentent, les valeurs de \(f(x)\) diminuent :
Appliquer à des nombres la fonction f change leur ordre.
Exemple :
On le reverra plus tard, mais on peut dire dès maintenant que la fonction \(x \to \frac 1 x\) est décroissante sur l'intervalle [1 ;10].
Donc, puisque \(2,3<5,7\), alors \(\frac 1 {2,3}>\frac 1 {5,7}\).