Dresser un tableau de variations
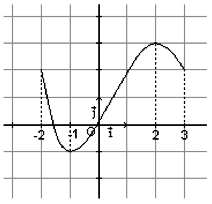
On considère la fonction f définie sur [-2 ;3] dont la courbe représentative est dessinée ci-contre.
Question
Dresser le tableau de variations de la fonction f.
Indice
Commencer par déterminer les intervalles sur lesquels f est monotone.
Indice
On n'oubliera pas de faire apparaître les images de f aux bornes des intervalles définis ci-dessus.
Solution
En observant la courbe, il semble intéressant d'étudier les variations de f sur les intervalles [-2 ;-1], [-1 ;2] et [2 ;3] :
f est décroissante sur [-2 ;-1]
f est croissante sur [-1 ;2]
f est décroissante sur [2 ;3]
d'autre part,
f(-2)=2
f(-1)=-1
f(2)=3
f(3)=2
Nous avons donc réuni les éléments pour dresser le tableau de variations ci-dessous :
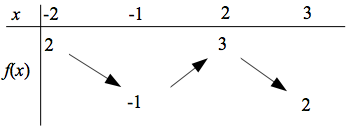
Question
En utilisant le tableau de variations, donner le nombre de solutions de l'équation f(x)=1 et les intervalles dans lesquelles elles se situent.
Indice
Examiner successivement chaque intervalle sur lequel f est monotone à la recherche d'une solution éventuelle.
Solution
Sur l'intervalle [-2 ;-1], la fonction f est décroissante de 2 à -1. Elle ne prend donc qu'une seule fois les valeurs de l'intervalle [-1;2]. Comme 1 est situé dans cet intervalle, on aura une première solution \(x_1\) de l'équation dans l'intervalle [-2 ;-1].
Sur l'intervalle [-1 ;2], la fonction f est croissante de -1 à 3. Elle ne prend donc qu'une seule fois les valeurs de l'intervalle [-1 ;3]. Comme 1 est situé dans cet intervalle, on aura une deuxième solution \(x_2\) de l'équation dans l'intervalle [-1 ;-2].
Sur l'intervalle [2 ;3], la fonction f est décroissante de 3 à 2. Elle n'atteint donc jamais la valeur 1. L'équation f(x)=1 n'a donc pas de solutions dans cet intervalle.
En conclusion, le tableau de variation nous permet de dire que f(x)=1 admet une solution \(x_1\) entre -2 et -1 et une solution \(x_2\) entre -1 et 2.