Expérience comportant plusieurs épreuves
Regarder la vidéo suivante
Nous avons déjà rencontré des expériences de ce type lorsque par exemple nous avons lancé deux fois de suite une pièce de monnaie ou bien réalisé deux lancers de dés successifs.
Exemple : Expérience à deux épreuves
Je considère l'expérience suivante constituée de deux épreuves :
Première épreuve : On fait tourner une roue marquée sur ses secteurs de couleurs différentes et on regarde le secteur marqué par la flèche.
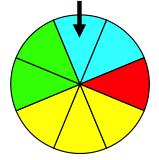
Seconde épreuve : On lance une pièce de monnaie bien équilibrée et on note la face obtenue.

Une issue de cette expérience est un couple de résultat du type (Couleur,face). Par exemple (Bleu,Pile) ou (Vert,Face)
L'univers Ω associé à cette expérience est l'ensemble de toutes les issues possibles.
Méthode : Représentation sous forme d'arbre
Dans le cas d'une expérience comportant plusieurs expériences successives, on a souvent recours à une représentation sous forme d'arbre pour représenter l'univers des issues possibles.
Exemple :
Dans l'exemple précédent, l'arbre représentant l'univers serait :
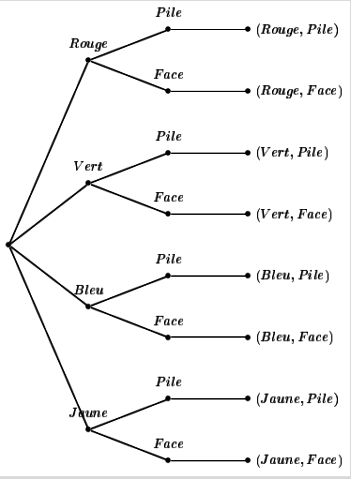
Les issues s'obtiennent au bout de chaque branche de l'arbre. On peut en dénombrer 8.
Pour retrouver facilement le nombre d'issues possibles, il suffit de remarquer que la première expérience donne lieu à 4 branches puisqu'elle comporte 4 issues et que la seconde divise chaque branche de la première en deux branches. Il y a donc au total \(4\times 2=8\) branches
Méthode :
Pour connaître le nombre d'issues pour une expérience comportant plusieurs épreuves, il suffit de multiplier les nombres d'issues possibles de chacune des épreuves.
Complément : Arbre pondéré
On peut ajouter au niveau de chaque branche de l'arbre les probabilités des issues associées. On obtient ainsi un arbre pondéré.
Exemple :
Dans la situation précédente, l'arbre pondéré serait
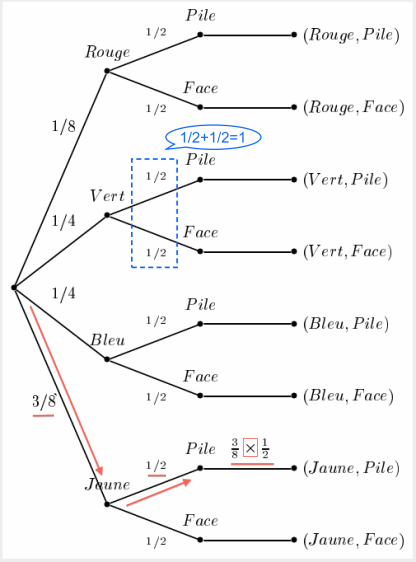
Sur cet arbre, on lit les deux propriétés fondamentales des arbres pondérés qui sont les suivantes :
Fondamental : Propriétés des arbres pondérés
Propriété 1 : La probabilité d'un événement est le produit des probabilités rencontrées sur le chemin conduisant à cet événement. Dans l'exemple précédent, on a\( \mathbb P(Jaune,Pile)=\dfrac{3}{8}\times \dfrac{1}{2}=\dfrac{3}{16}\)
Propriété 2 : la somme des probabilités de toutes les branches issues d'un même nœud est égal à 1. Exemple : \(\dfrac{1}{2}+\dfrac{1}{2}=1\) mais aussi sur le noeud de départ : \(\dfrac{1}{8}+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{3}{8}=1\)