On considère l'expérience suivante constituée de deux épreuves :
Épreuve 1 : On lance un dé bien équilibré et on regarde si la face obtenue est multiple de 3 (On notera M cet événement)
Épreuve 2 : On lance une pièce de monnaie et on notera la face P ou F.
Question
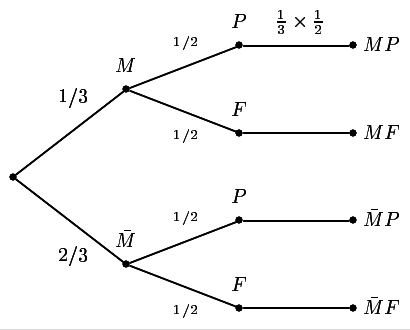
Écrire l'arbre pondéré représentant cette expérience.
Combien y a t-il d'issues possibles ?
Indice
Il y a deux multiples de 3 : 3 et 6.
Solution
La probabilité de l'événement M est la somme des probabilités de l'issue 3 et de l'issue 6. C'est donc \(\mathbb P(M)=\dfrac{1}{6}+ \dfrac{1}{6}=\dfrac{1}{3}\)
Sur la branche corresspondant à \(\bar M\) nous avons donc \(1-\dfrac{1}{3}=\dfrac{2}{3}\) puisqu'on sait que sur le noeud de départ, la somme des probabilités vaut 1.
Pour le pile ou face c'est une chance sur deux à chaque fois. L'arbre se déduit donc facilement.
Question
Quelle est la probabilité d'obtenir un multiple de 3 et Pile ?
Solution
Sur l'arbre, nous voyons que \(\mathbb P(M,P)=\dfrac{1}{3}\times \dfrac{1}{2}=\dfrac{1}{6}\)