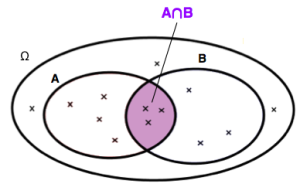
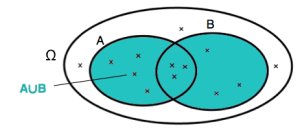
Union, intersection
Regardez la vidéo
Voir vidéo de 35.30 minutes à 43 minutes
Exemple : Lancer d'un dé
On lance un dé équilibré à 6 faces. On note les événements
A : « le numéro obtenu est impair »
B : « le numéro obtenu est inférieur ou égal à 4 »
A = {1; 3; 5}
B = {1; 2; 3; 4}
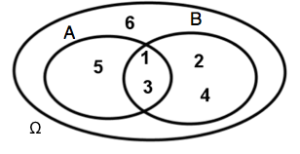
On peut représenter les événements A et B sous forme d'un diagramme.
On voit sur le diagramme que
les issues 1 et 3 appartiennent à A et à B
les issues 1, 2 3 4 et 5 appartiennent à A ou à B
On obtient ainsi à partir de A et B deux nouveaux événements.
Le premier {1 ;3} sera l'intersection de A et B
Le second {1 ;2 ;3 ;4 ;5} sera la réunion de A et B
Définition : Union, intersection d'événements
L'événement "A et B" est constitué des issues réalisant à la fois l'événement A et l'événement B.
On le note \(A\cap B\) qui se prononce « A inter B »
L'événement "A ou B" est constitué des issues réalisant l'événement A ou l'événement B.
On le note \(A\cup B\) qui se prononce « A union B »
Exemple : Calcul de probabilités
Nous avions dans l'exemple précédent
A = {1; 3; 5} donc \(\mathbb P(A)=\dfrac{3}{6}\)
B = {1; 2; 3; 4} donc \(\mathbb P(B)=\dfrac{4}{6}\)
\(A\cup B={1 ;2 ;3 ;4 ;5}\) donc \(\mathbb P(A\cup B)=\dfrac{5}{6}\)
\(A\cap B={1 ;3}\) donc \(\mathbb P(A\cap B)=\dfrac{2}{6}\)
On peut constater sur cet exemple que \(\mathbb P(A\cap B) + \mathbb P(A\cup B)=\mathbb P(A)+\mathbb P(B)=\dfrac{7}{6}\)
Ce résultat est une propriété fondamentale des probabilité. Nous pouvons l'énoncer ainsi
Fondamental : Propriété à retenir
Si A et B sont deux événements, alors \(\mathbb P(A\cup B)=\mathbb P(A)+\mathbb P(B) - \mathbb P(A\cap B)\)