Forme Canonique
Fondamental : Propriété
Tout polynôme du second degré peut se mettre sous la forme :
\(f(x)=a(x-\alpha)^2+\beta\) où \(\alpha=-\frac{b}{2a}\) et \(\beta=f(\alpha)\).
Cette forme est appelée forme canonique.
Exemple :
\(f(x)=x^2-2x+1\)
Sans utiliser la formule ci-dessus, on a : \(f (x) = (x − 1)^2\). On va vérifier qu'il s'agit bien de la forme canonique.
Ici: \(a=1;b=−2 ; c=1\). On a bien: \(\alpha=-\frac{b}{2a} =-\frac{-2}{2}=1\) et \(\beta=f(1)=1^2−2×1+1=0\)
La forme canonique est donc bien : \(f (x) = (x − 1)^2 + 0\).
Exemple :
\(f(x)=2x^2 −6x+1\)
Ici: \(a=2 ,\ b=−6\ et\ c=1\). On a donc : \(\alpha=-\frac{b}{2a} =-\frac{-6}{2\times 2}=\frac{3}{2}\) et \(\beta=f(\frac{3}{2})=2\times \left(\frac{3}{2}\right)^2−6×\frac{3}{2}+1=-\frac{7}{2}\).
La forme canonique est donc : \(f (x) = 2 \left(x − \frac{3}{2} \right) ^2 -\frac{7}{2}\).
Définition :
La courbe représentative du trinôme du second degré est appelée Parabole. Cette parabole admet pour sommet le point S de coordonnées \((\alpha,\beta)\).
Remarque :
Le mot parabole rappelle l'antenne de réception de la TV par satellite :
En effet, la forme de l'antenne est une parabole, qui a la particularité de concentrer toutes les ondes provenant du satellite en un seul point, où on place le récepteur.
C'est aussi le principe des fours paraboliques qu'on trouve en montagne :
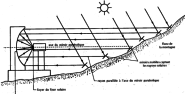
Remarque :
Pour un polynôme du second degré, il existe donc une forme réduite (celle de la définition, c'est la forme développée), une forme canonique et éventuellement une forme factorisée. Suivant le problème posé, il faudra donc choisir entre ces formes.
Simulation : Influence des coefficients α, ß et a
Remarque : Cas d'utilisation des différentes formes
Pour trinôme donné \(P(x)\), on utilisera plutôt :
Sa forme développée : pour calculer l'image de 0 par \(P\),
sa forme canonique pour résoudre par exemple \(P(x)=0\),
sa forme canonique pour déterminer le tableau des variations de \(P\),
on choisit la forme la plus adaptée selon les cas.
Fondamental : Mise sous forme canonique dans le cas général
Transformation de l'écriture \(ax²+ bx + c\) :
On met a en facteur (possible car \(a\neq0\)) :
\(a(x²+\frac{b}{a}x+\frac{c}{a})\)
Or, \(x²+\frac{b}{a}x=\left(x+\frac{b}{2a}\right)^2-\frac{b²}{4a²}\)
D'où \(a\left(x²+\frac{b}{a}x+\frac{c}{a}\right)=a\left[\left(x+\frac{b}{2a}\right)^2-\frac{b²}{4a²}+\frac{c}{a}\right]=a\left[\left(x+\frac{b}{2a}\right)^2-\frac{b²-4ac}{4a²}\right]\)
Pour simplifier l'écriture, on pose \(\Delta=b²-4ac\).
On obtient donc :
\(ax²+bx+c=a\left[\left(x+\frac{b}{2a}\right)^2-\frac{\Delta}{4a²}\right]\)
Ainsi, \(\beta=\frac{-\Delta}{4a}\)
Complément :
Cette forme canonique va nous servir dans au moins quatre cas :
dire si le trinôme possède ou non des racines, et lesquelles s'il en a ;
factoriser le trinôme lorsque ce sera possible ;
connaître le signe du trinôme suivant les valeurs de \(x\);
étudier les variations de la fonction \(P\) définie par \(P(x) = ax²+ bx + c\) et tracer l'allure de sa représentation graphique (coordonnées de l'extremum) et en calculant f(0), qui vaut en fait le coefficient c, on a un autre point de la courbe.
Le symétrique de ce dernier par rapport à l'axe de symétrie est aussi un point de la courbe.
