Exercice : Approche intuitive
Dans cette activité, nous allons étudier plusieurs comportements en l'infini.
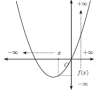
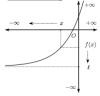
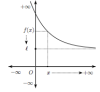
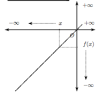
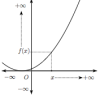
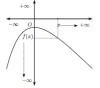
Glisser les différentes courbes dans la catégorie qui leur correspond en fonction du comportement de la fonction en l'infini.
Plus d'éléments à catégoriser | Les images de \(x\) par la fonction \(f\) s'approchent d'un réel \(\ell\) lorsque \(x\) tend vers \(+\infty\) : \(\lim\limits_{x \to +\infty} f(x)=\ell\) Déposez ici Les images de \(x\) par la fonction \(f\) s'approchent d'un réel \(\ell\) lorsque \(x\) tend vers \(-\infty\) : \(\lim\limits_{x \to -\infty} f(x)=\ell\) Déposez ici Les images de \(x\) par la fonction \(f\) tendent vers \(+\infty\) lorsque \(x\) tend vers \(+\infty\) : \(\lim\limits_{x \to +\infty} f(x)=+\infty\) Déposez ici Les images de \(x\) par la fonction \(f\) tendent vers \(-\infty\) lorsque x tend vers \(-\infty\) : \(\lim\limits_{x \to -\infty} f(x)=-\infty\) Déposez ici Les images de \(x\)par la fonction \(f\) tendent vers \(+\infty\) lorsque \(x\) tend vers \(-\infty\) : \(\lim\limits_{x \to -\infty} f(x)=+\infty\) Déposez ici Les images de \(x\)par la fonction \(f\) tendent vers \(-\infty\) lorsque \(x\) tend vers \(+\infty\) : \(\lim\limits_{x \to +\infty} f(x)=-\infty\) Déposez ici |
