Limite finie en l'infini
Définition :
Si \(f\) est une fonction définie sur un intervalle \(]a ;+\infty[\), \(f\) a pour limite le réel \(\ell\) quand \(x\) tend vers l'infini si les images \(f(x)\) sont aussi proches que l'on veut de \(\ell\), à condition de prendre \(x\) suffisamment grand.
On note alors \(\lim\limits_{x \to +\infty} f(x)=\ell\)
On peut formaliser les choses en s'inspirant de la définition donnée pour les limites finies de suites :
\(\lim\limits_{x \to +\infty} f(x)=\ell\) si pour tout intervalle ouvert \(I_\epsilon=]\ell-\epsilon ;\ell+\epsilon[\), il existe un réel m tel que \(f(x)\in I_\epsilon\) dès que \(x>m\)
Complément :
La droite d'équation \(y=\ell\) est alors une asymptote horizontale à la courbe en \(+\infty\).
Exemple :
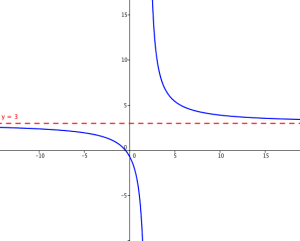
Avec la fonction homographique de l'activité précédente, on a \(\lim\limits_{x \to +\infty} f(x)=3\) mais on peut aussi montrer de manière analogue que \(\lim\limits_{x \to -\infty} f(x)=3\).
Par conséquent, la droite d'équation \(y=3\) est asymptote horizontale à la courbe \(\mathcal C_f\) en \(-\infty\) et en \(+\infty\).
Graphiquement, la courbe s'approche de la droite autant que l'on souhaite, sans toutefois ne jamais la toucher comme on l'a démontré dans l'activité précédente.
Fondamental : Limite de référence
\(\lim\limits_{x \to -\infty} \frac{1}{x}=0\) et \(\lim\limits_{x \to +\infty} \frac{1}{x}=0\).
Par conséquent l'axe des abscisses est asymptote horizontale pour la courbe représentative de la fonction inverse.
Attention :
Certaines fonctions n'ont pas de limite, finie ou infine en l'infini. C'est le cas par exemple des fonction sin et cos qui oscillent sans arrêt.