Approche d'une limite finie en l'infini
On considère la fonction définie sur \(]2 ;+\infty[\) par \(f :x\longmapsto \frac{9x+4}{3x-6}\)
Question
A l'aide de la calculatrice, conjecturer la limite de \(f\) en \(+\infty\).
Indice
On pourra calculer des images par \(f\) de nombres de plus en plus grand.
Solution
On calcule à l'aide de la calculatrice :
\(f(100)\approx 3,075\)
\(f(1000)\approx 3,007\)
\(f(1000000)\approx 3,00001\)
On peut donc émettre la conjecture que les images de \(x\) s'approche de 3 lorsque \(x\) tend vers l'infini.
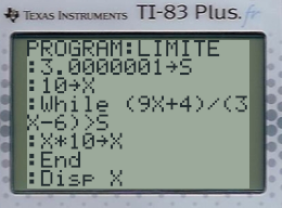
Cette conjecture ne constitue en rien une preuve. Néanmoins, si elle est vraie, cela signifie qu'on peut s'approcher de la valeur obtenue autant que l'on souhaite. Vérifions cela à l'aide d'un algorithme :
S prend la valeur 3,0000001
X prend la valeur 10
Tant Que f(X)>S
... X prend la valeur X*10
Afficher X
Question
Quel est le rôle de cet algorithme ? A quoi servent les variables ?
Expliquer le choix de la méthode utilisée.
Solution
Cet algorithme permet de savoir si on peut s'approcher de 3 à une distance de moins de 0,0000001.
Dans cet algorithme S désigne le seuil d'approche de la valeur limite 3. X désigne un nombre de plus en plus grand.
La convergence de la fonction vers le nombre 3 peut être assez lente (on l'a vu avec f(1000000)). Pour éviter à la calculatrice de faire des millions de passage dans la boucle et tourner pendant des heures, on donne à X des valeurs de plus en plus grandes en le multipliant par 10 à chaque passage. On obtient ainsi une croissance exponentielle nous permettant de nous approcher plus vite de l'infini.
Question
Question
Résoudre l'équation \(f(x)=3\).
Interpréter ce résultat.
Solution
si \(x\neq 2, \frac{9x+4}{3x-6}=3 \Longleftrightarrow 9x+4=3(3x-6)\)
donc si \(x\neq 2, \frac{9x+4}{3x-6}=3 \Longleftrightarrow 9x+4=9x-18\) c'est à dire \(4=-18\) ! !
l'équation \(f(x)=3\) n'a donc pas de solutions.
On peut en conclure que même si on peut s'approcher de 3 autant que l'on souhaite, il n'est pas possible pour f d'atteindre exactement la valeur 3. La limite d'une fonction n'est pas nécessairement une valeur prise par la fonction.
Question
Calculer \(f(10^{11})\). Conclure.
Solution
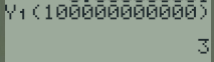
La calculatrice semble montrer que \(f(10^{11})=3\). Néanmoins, l'équation que nous venons de résoudre montre que cela est impossible, la valeur 3 ne pouvant être atteinte par f.
Il faut donc en conclure qu'il faut être critique à l'égard des résultats fournis par la calculatrice. Ceux-ci sont toujours des valeurs approchées.
Nous allons à présent démontrer rigoureusement notre conjecture. Pour cela, nous allons montrer que nous pouvons nous approcher aussi près que l'on veut de la limite 3, dès lors que \(x\) est suffisamment grand.
Question
Montrer que \(f(x) > 3\) pour tout réel de \(]2 ;+\infty[\).
Solution
si \(x\in]2 ;+\infty[\), on a \(3x-6 >0\). Par conséquent :
si \(x\in]2 ;+\infty[, \frac{9x+4}{3x-6}>3 \Longleftrightarrow 9x+4>3(3x-6)\Longleftrightarrow 4>-18\)
Or cette inégalité est toujours vraie pour \(x>2\), ce qui démontre le résultat cherché.
Question
Montrer qu'il existe un nombre m tel que si \(x>m, 0<f(x)-3<10^{-n}\) pour n'importe quelle valeur de \(n\).
Interpréter ce résultat.
Solution
\(f(x)-3=\frac{9x+4}{3x-6}-3=\frac{9x+4}{3x-6}-\frac{9x-18}{3x-6}=\frac{22}{3x-6}\)
Par conséquent \(f(x)-3<10^{-n}\Longleftrightarrow \frac{22}{3x-6}<10^{-n}\).
Or si \(x>2\), alors \(3x-6>0\) donc l'inéquation se ramène par produit par \((3x-6)\times 10^n\) à \(22\times 10^n<3x-6\)
donc \(x>\frac{22\times 10^n+6}{3}\)
Posons \(m=\frac{22\times 10^n+6}{3}\), si \(x>m\), on vient de démontrer que \(f(x)-3<10^{-n}\)
On peut donc s'approcher avec la précision que l'on veut de la valeur 3, à condition de prendre \(x\) suffisamment grand.
Cela montre donc que la limite de la fonction f est 3 en \(+\infty\).