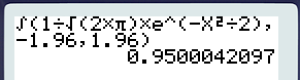Calculer avec la loi normale
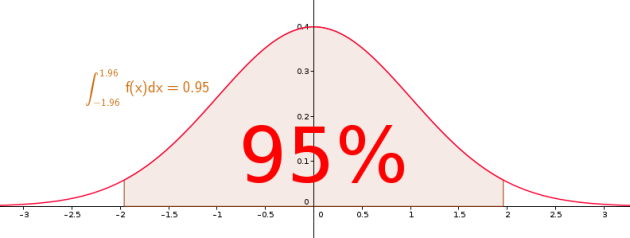
On considère une variable aléatoire X suivant la loi normale centrée réduite :
\(X\hookrightarrow \mathcal N(0 ;1)\)
Question
Calculer \(\mathbb P(-1,96\leqslant X\leqslant 1,96)\).
Ce résultat sera à retenir.
Indice
On pourra utiliser la fonction intégrale de la calculatrice ou la fonction "loi normale".
Solution
A l'aide de geogebra, on détermine que \(\mathbb P(-1,96\leqslant X\leqslant 1,96)=0,95\) soit une probabilité de 95%.
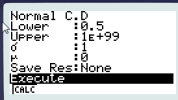
Avec la TI
La fonction normalpdf( se trouvant dans le menu \(\fbox{distrib}\) est la fonction densité de la loi normale. Par conséquent, la commande ci-contre fournit également le résultat escompté.
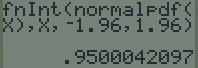
La fonction normalcdf( se trouvant à coté permet de calculer la probabilité. Voici comment elle s'utilise :
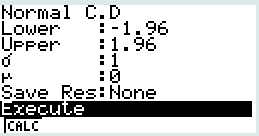
Avec la Casio
Aller dans le \(\fbox{MENU}~ STAT 2\) puis \(\fbox{F5}~ DIST~ ~ \fbox{F5} ~ NORM~ ~ \fbox{F1}~Ncd\). On remplit ensuite les paramètres comme indiqués ci-contre :
Le résultat est alors disponible sur l'écran ci-contre :
On peut aussi utiliser la fonction de Gauss \(f : x \longmapsto \frac{1}{\sqrt{2\pi}}~e^{\frac{-x²}{2}}\) et son intégrale entre -1,96 et 1,96 :
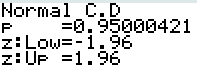
Question
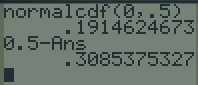
Calculer\(\mathbb P(X\leqslant 1)\).
Indice
Ne pouvant mettre \(-\infty\) comme borne inférieure, on pourra remarquer que grâce à la relation de Chasles, \(\mathbb P(X\leqslant 1)=\mathbb P(X\leqslant 0)+\mathbb P(0\leqslant X\leqslant 1)\)
Solution
On sait que \(\mathbb P(X\leqslant 0)=\dfrac{1}{2}\)
On calcule \(\mathbb P(0\leqslant X\leqslant 1)\approx 0,3413\)
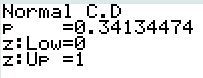
Donc \(\mathbb P(X\leqslant 1)\approx 0,8413\)
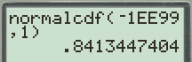
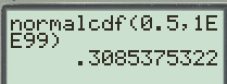
On peut aussi calculer en prenant pour valeur inférieure \(-1\times 10^{99}\) qui est un nombre très petit et 1 :
Question
Calculer \(\mathbb P(X\geqslant 0,5)\).
Indice
Ne pouvant indiquer \(+\infty\) comme borne supérieure, on remarquera que \(\mathbb P(X\geqslant 0,5)=\mathbb P(X\geqslant 0)-\mathbb P(0\leqslant X\leqslant 0,5)\).
Solution
On sait que \(\mathbb P(X\geqslant 0)=0,5\)
On calcule \(\mathbb P(0\leqslant X\leqslant 0,5)\approx 0.1915\)
Par conséquent \(\mathbb P(X\geqslant 0,5)\approx 0,5-0,1915\approx 0,3085\).
On peut aussi calculer ainsi :
ou sur casio :
