Fonction exponentielle
Fondamental : Propriété (admise)
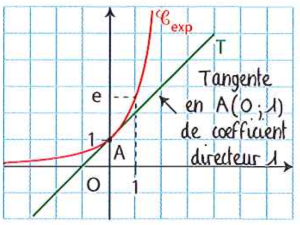
Il existe une seule valeur du réel \(q\) telle que la tangente au point A(0 ; 1) à la courbe représentative de la fonction \(x\longmapsto q^x\) ait pour coefficient directeur 1.
Définition : fonction exponentielle de base e
Cette valeur particulière du réel \(q\) est notée e. Le réel e est égal à environ 2,71828.
Ce nom a été choisi par le mathématicien Leonhard Euler :
![]()
La fonction \(x\longmapsto e^x\) s'appelle fonction exponentielle de base e ou plus simplement fonction exponentielle. On la note \(exp : x\longmapsto e^x\)
Complément : Conséquences
La fonction exponentielle est définie sur \(\mathbb{R}\) par \(exp(x)=e^x\).
La fonction exp est dérivable sur \(\mathbb{R}\) et son nombre dérivé en 0 est 1.
La fonction exp est strictement positive sur \(\mathbb{R}\) : pour tout réel \(x\), \(e^x>0\).
\(e>1\) donc la fonction exp est strictement croissante sur \(\mathbb{R}\). On en déduit que :
\(e^a=e^b\) si et seulement si \(a=b\),
\(e^a < e^b\) si et seulement si \(a<b\) (exp conserve l'ordre des inégalités).
Les propriétés algébriques des fonctions exponentielles de base q s'appliquent à la fonction exp :
Pour tous nombres \(x\) et \(y\) réels, on a :
\(e^{x+y}=e^x\times e^y\) : la fonction exponentielle transforme les sommes en produits
\(e^{-x}=\dfrac{1}{e^x}\)
\((e^x)^n=e^{nx}\)
\((e^x)^y=e^{xy}=(e^y)^x\)
Exemple : Avec la calculatrice
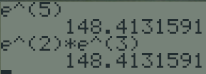
\(e^5=e^2\times e^3\)
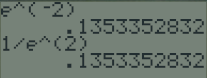
\(e^{-2}=\dfrac{1}{e^2}\)
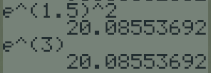
\((e^{1,5})^2=e^3\)
