Etude d'une fonction
Étude de la fonction \(f :x\longmapsto xe^x\)
Question
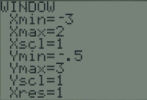
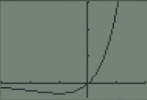
Quel est l'ensemble de définition de f et tracer la courbe sur la calculatrice.
Solution
La fonction f est définie sur \(\mathbb{R}\) car produit de deux fonctions définies chacune pour tout réel. Traçons la courbe représentative de f sur la calculatrice. Il conviendra de régler l'échelle convenablement pour bien visualiser les variations de la fonction.
|
|
Question
Étudier les variations de la fonction \(f\) et confronter les résultats au graphique obtenu ci-dessus.
Indice
Calculer la dérivée de la fonction. Il s'agit du produit de deux fonctions (que l'on sait dériver).
Solution
\(f'(x)=1\times e^x+x\times e^x=(1+x)e^x\)
La fonction exponentielle étant toujours positive, le signe de \(f'\) est le signe de \(x+1\) donc négatif jusqu'à -1 puis positif.
On en déduit le tableau de variation ci-dessous, ce qui confirme le graphique obtenu sur la calculatrice.
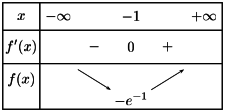
La fonction est donc décroissante sur ]-∞ ;-1[ puis croissante sur ]-1 ; +∞ [. En -1, elle admet un minimum car la dérivée s'annule et change de signe.