Propriété fondamentale
Soit \(q\) un réel différent de 1 et \((u_n)\) une suite géométrique de raison \(q\). On va s'intéresser ici à la somme des \(n\) premiers termes de la suite \((u_n)\) :
Posons \(S=1+q+q^2+ ... + q^n\).
On peut calculer \(qS=q+q^2+q^3+ ... +q^{n+1}\)
Retranchons ces deux expressions :
\(S-qS=1+q+q^2+...+q^n-q-q^2- ... -q^n-q^{n+1}\)
On constate que presque tous les termes s'éliminent. Ne restent que les extrêmes :
\(S-qS=S(1-q)=1-q^{n+1}\)
Ce qui permet de calculer S : \(S=\dfrac{1-q^{n+1}}{1-q}\) car \(q≠1\)
Fondamental : Somme des n premiers termes d'une suite géométrique
Soit q un réel différent de 1 et \((u_n)\) une suite géométrique de raison q. Alors pour tout entier n :
\(1+q+q^2+ ... + q^n=\dfrac{1-q^{n+1}}{1-q}\)
On en déduit en multipliant par \(u_0\) cette égalité que :
\(u_0+u_1+u_2+ ... +u_n=u_0\dfrac{1-q^{n+1}}{1-q}\)\(=1^{er}\ terme\times\dfrac{1-raison^{nombre\ de\ termes}}{1-raison}\)
Exemple : Calculer la somme des 10 premières puissances de 2.
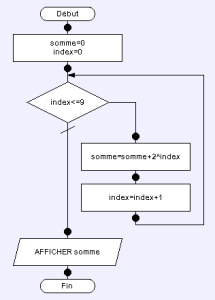
On peut également vérifier cela à l'aide d'un programme correspondant à l'algorithme ci-contre.
Nous pouvons le langage Python pour implémenter cet algorithme.
On remarquera au passage l'utilisation de la boucle "for" avec comme paramètre range(10) pour exécuter 10 fois la section contenue dans le bloc.
range(10) retourne une liste des 10 premiers entiers commençant à 0 :
>>> range(10)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
somme=0
for index in range(10):
somme=somme+2**index
print somme
>>> 1023
On peut le calculer mathématiquement à l'aide de la propriété vue ci-dessus.
On pose \(u_n=2^n\) la suite géométrique de raison 2 et de premier terme 1.
Alors \(1+2+2^2+2^3+ ... +2^9=1\dfrac{1-2^{10}}{1-2}=\dfrac{1-1024}{1-2}=1023\)
En utilisant la calculatrice, on peut procéder ainsi :
Avec une TI :
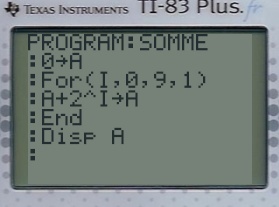
Avec une casio :
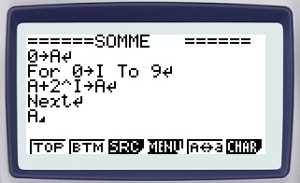
En utilisant algobox, on peut procéder ainsi :