Une propriété de ln
On sait que la fonction exponentielle est concave sur \(]0 ;+\infty[\), ce qui signifie qu'elle est toujours au dessous de ses tangentes en n'importe quel point.
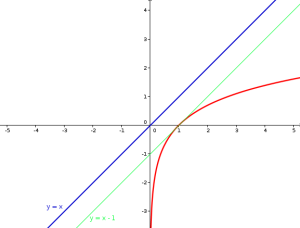
Or nous connaissons une tangente à l'équation particulièrement simple : la tangente en 1 dont l'équation est \(y=x-1\).
Donc pour tout réel \(x\), \(\ln x\leqslant x-1\).
Mais on sait aussi que \(x-1<x\) ! On en déduit donc la propriété fondamentale suivante :
Complément :
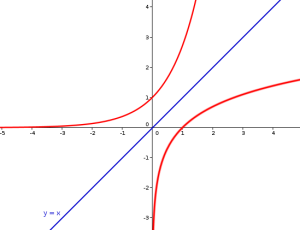
On retrouve ici quelque chose de familier lorsque l'on a construit la courbe de la fonction logarithme par symétrie de la courbe de exponentielle par rapport à la droite y=x.