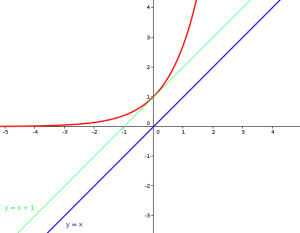
Une propriété de exp
On sait que la fonction exponentielle est convexe sur \(\mathbb R\), ce qui signifie qu'elle est toujours au dessus de ses tangentes en n'importe quel point.
Or nous connaissons une tangente à l'équation particulièrement simple : la tangente en 0 dont l'équation est \(y=x+1\).
Donc pour tout réel \(x\), \(e^x\geqslant x+1\).
Mais on sait aussi que \(x+1>x\) ! On en déduit donc la propriété fondamentale suivante :
Fondamental : exp(x) est plus fort que x ! !
Pour tout réel \(x\), \(e^x>x\)