Nous allons voir dans cet exemple une application des inégalités vues dans ce paragraphe au travers de l'étude de la fonction \(f :x\longmapsto e^ x-\dfrac{x^2}{2}+3\)
Question
A l'aide de la calculatrice, conjecturer le sens de variation de la fonction \(f\).
Solution
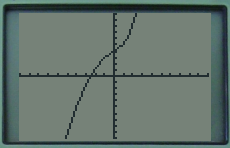
La lecture de la courbe semble montrer que la fonction est croissante sur \(\mathbb R\). Elle semble aussi mettre en évidence un point d'inflexion autour de \(x=0\).
Question
Démontrer la conjecture réalisée sur les variations de la fonction \(f\).
Solution
\(f'(x)=e^x-x\). On sait que l'exponentielle est supérieur à \(x\longmapsto x\), par conséquent \(f'(x)\) est positive pour tout réel. On en déduit donc que \(f\) est croissante sur \(\mathbb R\).
Question
Rechercher la présence de points d'inflexions.
Solution
\(f''(x)=e^x-1\).
Le cours sur la fonction exponentielle nous montre que f'' s'annule et change de signe pour x=0 puisque exponentielle est strictement croissante et que e^0=1.
Nous en déduisons la présence d'un point d'inflexion au point d'abscisse 0.