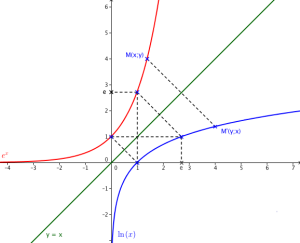
Courbe représentative de f(x)=ln x
Simulation : Activité de découverte de la courbe de la fonction ln
Déplacer le curseur pour modifier le nombre k.
La figure illustre la résolution graphique de \(e^x=k\).
Cochez la case M' pour faire apparaître le point de coordonnées \(M' (k;\ln k)\).
Découverte de la courbe représentative de la fonction Logarithme népérien à partir de la courbe de la fonction exponentielle
Remarque :
On voit en cochant le point M' et en bougeant le curseur k que la courbe de la fonction Logarithme Népérien apparaît point par point. Compte tenu de la manière dont le point M' est construit à partir du point M, on voit se dégager une propriété fondamentale :
Fondamental :
Remarque :
De même que la courbe de la fonction exponentielle ne passe jamais "sous" l'axe des abscisses, la courbe de la fonction logarithme népérien ne franchit jamais l'axe des ordonnées (partie gauche) car la fonction n'est pas définie pour les réels négatifs, ni même en 0. La courbe se rapproche de l'axe sans jamais le toucher.