Formules d'addition
Fondamental :
Soit \(a, b \in \mathbb R\)
\(\cos(a-b) = \cos a \cos b + \sin a \sin b\)
\(\cos(a+b) = \cos a \cos b - \sin a \sin b\)
\(\sin(a-b) = \sin a \cos b - \cos a \sin b\)
\(\sin(a+b) = \sin a \cos b + \cos a \sin b\)
Démonstration au programme
On considère un repère orthonormé \((O ;\overrightarrow i ; \overrightarrow j)\). \(\overrightarrow u\) et \(\overrightarrow v\) sont deux vecteurs de norme 1 tels que \((\overrightarrow i ; \overrightarrow u) = a\) et \((\overrightarrow i ; \overrightarrow v) = b\)
On a alors \(\overrightarrow{u} \left (\begin{array}{c}\cos a \\ \sin a\end{array}\right )\) et \(\overrightarrow{v} \left (\begin{array}{c}\cos b \\ \sin b\end{array}\right )\)
Ainsi \(\overrightarrow{u} \cdot \overrightarrow{v} = \cos a \cos b - \sin a \sin b\)
Mais on a aussi \(\overrightarrow{u} \cdot \overrightarrow{v} =||\overrightarrow{u} ||\times ||\overrightarrow{v}||\times \cos(\overrightarrow u ; \overrightarrow v)= 1 \times 1 \times \cos(a-b)\) ce qui nos donne la première formule
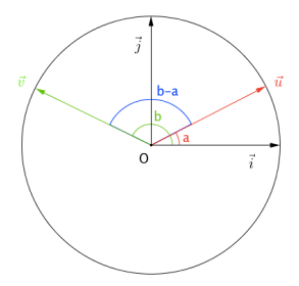
Les autres formules vont s'en déduire en utilisant les propriétés des fonction cos et sin
\(\cos(a+b) = \cos(a-(-b)) = \cos a \cos (-b) + \sin a \sin (-b) = \cos a \cos b - \sin a \sin b\)
\(\sin(a-b) = \cos\left( \dfrac \pi 2 - (a-b)\right)\)
\(\sin(a-b) = \cos\left(\dfrac \pi 2-a\right) \cos b - \sin\left(\dfrac \pi 2-a\right) \sin b\)
\(\sin(a-b) = sin a \cos b - \cos a \sin b\)
\(\sin(a + b) = \sin (a - (-b)) = \sin a \cos(-b) - \cos a \sin(-b) = \sin a \cos b + \cos a \sin b\)