Résoudre une équation trigonométrique
Question
Résoudre dans \([0 ; 2\pi]\) l'équation \(cos(2x) = sin x\).
Indice
On pourra écrire cette équation en utilisant que \(\sin x\) puis résoudre une équation du second degré
Solution
\(cos(2x) = sin x \Longleftrightarrow 1-2\sin^2 x = \sin x\)
Posons \(X=\sin x\), on se ramère à une équation du second degré :
\(2X^2+X-1=0\)
Résolvons cette équation : \(\Delta = 9\) donc les 2 solutions sont \(X_1=\dfrac 1 2\) et \(X_2=-1\)
Pour revenir à \(x\) on doit alors résoudre deux équations à base de sin
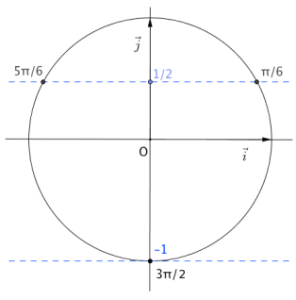
\(\sin x=\dfrac 1 2\) pour \(x=\dfrac \pi 6\) ou \(x=\dfrac{5\pi}6\)
\(\sin x = -1\) pour \(x=\dfrac {3\pi}2\)
Conclusion
L'équation possède 3 solutions sur \([0 ; 2\pi]\) : \(\dfrac \pi 6\), \(\dfrac{5\pi}6\) et \(\dfrac{3\pi}2\)