Calcul du coefficient directeur
Nous avons vu dans le chapitre sur les fonctions affines une formule permettant de calculer le coefficient directeur connaissant deux nombres et leurs images. Cette formule s'applique également dans le cadre de ce chapitre lorsque l'on connaît les coordonnées de deux points sur une droite.
Fondamental :
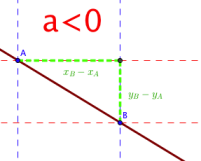
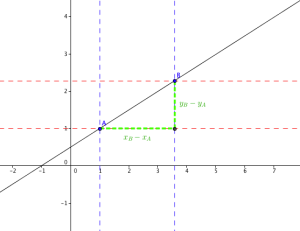
Dans un repère, si \(A(x_A ;y_A)\) et \(B(x_B ;y_B)\) sont deux points tels que \(x_A\neq x_B\),
alors, le coefficient directeur de la droite (AB) se calcule par la formule \(a=\dfrac{y_B-y_A}{x_B-x_A}\).
Si, dans un repère, les coordonnées de deux points \(A(x_A ;y_A)\) et \(B(x_B ;y_B)\) sont tels que \(x_A= x_B\), alors la droite a pour équation :
\(x=x_a\).
Par exemple, l'axe des ordonnées a pour équation \(x=0\).
Complément : Démonstration
Soit \(y=ax+b\) l'équation de la droite (AB) (celle-ci est par hypothèse non parallèle à l'axe des ordonnées car \(x_A\neq x_B\)).
Nous avons alors \(A\in(AB)\) donc ses coordonnées vérifient l'équation \(y_A=ax_A+b\).
Nous avons de même \(B\in(AB)\) donc ses coordonnées vérifient l'équation \(y_B=ax_B+b\).
En faisant la différence de ces deux équations, nous obtenons une nouvelle équation dans laquelle l'inconnue b s'élimine : \(y_B-y_A=a(x_B-x_A)\).
Il ne reste plus qu'à faire le quotient par \((x_B-x_A)\) non nul par hypothèse pour isoler notre inconnue a.
\(a=\dfrac{y_B-y_A}{x_B-x_A}\) ce qui donne bien la formule désirée.
Remarque :
Le coefficient directeur s'interprète donc comme le quotient du déplacement vertical sur le déplacement horizontal.
Complément :
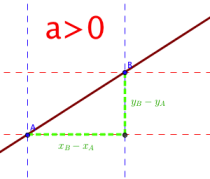
Si a>0, la droite "monte" quand on lit de la gauche vers la droite.
Si a<0, la droite "descend" quand on lit de la gauche vers la droite.
