Tracé de droites
En cas de difficultés pour faire cet exercice, vous pourrez consulter la vidéo ci-dessous
Question
Dans un repère, tracer les droites :
\((d_1) : y=2x+1\)
\((d_2) : y=-\dfrac{5}{3}x+3\)
\((d_3) : x=2\)
\((d_4) : y=-3\)
Indice
Pour la droite \((d_1)\), on pourra simplement exploiter les propriétés du coefficient directeur et de l'ordonnée à l'origine.
Indice
Pour la droite \((d_2)\), le coefficient directeur étant fractionnaire, on peut tenter de placer deux points de la droite dont les abscisses seront astucieusement choisies.
Indice
Pour \((d_3)\) et \((d_4)\), ces droites sont parallèles aux axes. Lesquels ?
Solution
Méthode : Méthode de construction
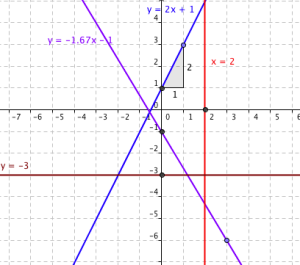
Pour la droite \((d_1)\), on place tout d'abord le point de coordonnées (0 ;1) correspondant à l'ordonnée à l'origine. Partant de ce point, on avance de une unité vers la droite et on monte de deux unités par lecture du coefficient directeur. Cela nous positionne le second point de la droite de coordonnées (1;3).
Pour la droite \((d_2)\), on place tout d'abord le point de coordonnées (0 ;-3) correspondant à l'ordonnée à l'origine. Ensuite, on va choisir le point d'abscisse 3 car 3 est le dénominateur de la fraction. En injectant x=3 dans l'équation de \((d_2)\), on obtient une ordonnée entière pour le second point de la droite : \(y=-\dfrac{5}{3}\times 3 +3=-5+3=-2\) d'où le second point de coordonnées (3;-2).
Pour la droite \((d_3)\), on sait qu'une droite d'équation du type \(x=c\) est parallèle à l'axe des ordonnées. C'est donc la droite verticale qui coupe l'axe des abscisses au point d'abscisse \(x=2\).
Pour la droite \((d_4)\), on sait qu'une droite d'équation du type \(y=b\) est parallèle à l'axe des abscisses. C'est donc la droite horizontale qui coupe l'axe des ordonnées au point d'ordonnée \(y=-3\).