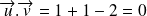Définition et propriétés
Définition :
Étant donnés deux vecteurs
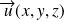 et
et
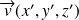 , on appelle produit scalaire de
, on appelle produit scalaire de
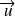 et
et
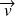 , noté
, noté
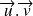 , le nombre réel :
, le nombre réel :
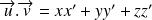
Exemple :
Avec
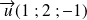 et
et
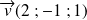 , on obtient
, on obtient
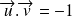 .
.
Complément :
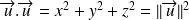 .
.
On note parfois ce nombre
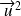 .
.
Fondamental : Expression du produit scalaire en fonction des normes des vecteurs.
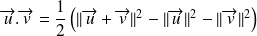
On démontrera cette formule en exercice.
Fondamental : Expression du produit scalaire en fonction de l'angle des vecteurs
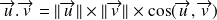
De cette relation, on en déduit cette propriété fondamentale du produit scalaire. En effet, le produit scalaire de deux vecteurs non nuls sera nul lorsque le cosinus de l'angle des deux vecteurs sera nuls donc lorsqu'ils formeront un angle de
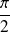 modulo
modulo
 .
.
Fondamental : Produit scalaire et orthogonalité
Les vecteurs non nuls
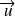 et
et
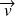 sont orthogonaux si et seulement si
sont orthogonaux si et seulement si
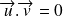 .
.
Exemple :
Si
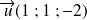 et
et
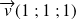
Alors
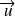 et
et
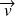 sont orthogonaux puisque
sont orthogonaux puisque