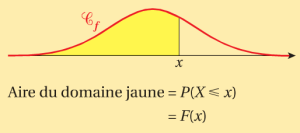
Densité de probabilité
De nouveaux univers
Jusqu'à présent, une expérience aléatoire conduisait à un univers fini et une variable aléatoire \(X\) prenait un nombre fini de valeurs. Nous avons vu dans l'exemple précédent qu'il arrive aussi que les issues d'une expérience aléatoire puissent être n'importe quel réel.
Adaptation du modèle
Dans ce cas, sa loi de probabilité, dite continue, n'est plus associée à la probabilité de chacune de ses valeurs mais à la probabilité d'intervalles de valeurs.
C'est par un calcul d'aire sous la courbe d'une fonction propre à chaque loi, appelée densité, que s'opèrent ces calculs. Une fonction de densité est une fonction continue, positive et dont l'aire totale sous sa courbe est égale à 1.
Définition : Densité de probabilité
L'activité précédente met en évidence une fonction \(f\) sur un intervalle \([a ;b]\) qui possède les caractéristiques suivantes :
\(f\) est une fonction continue et positive sur \([a ;b]\)
\(\displaystyle \int_a^b f(x)~dx=1\)
Toute fonction \(f\) qui remplit ces conditions sur un intervalle \([a ;b]\) est appelée densité de probabilité.
Complément :
Le fait que la fonction \(f\) soit continue sur \([a ;b]\) nous assure de pouvoir calculer les intégrales sur n'importe quel intervalle de \([a ;b]\).
Le fait que la fonction \(f\) soit positive nous assure de trouver une probabilité qui soit positive !
Le fait que \(\displaystyle \int_a^b f(x)~dx=1\) est imposé par le fait que la probabilité de l'événement certain est égale à 1.
Définition : Fonction de répartition
Soit \(X\) une variable aléatoire continue de densité \(f\).
La fonction de répartition associée à la variable aléatoire X est la fonction F définie sur \(\mathbb R\) par
\(F(x)=\mathbb P(X\leqslant x)\).