Activité d'approche : Du discret au continu
Rappel : Variable aléatoire discrète et loi de probabilité
Une variable aléatoire discrète ne peut prendre qu'un nombre fini de valeur réelles.
La loi de probabilité de cette variable aléatoire est le tableau donnant toutes les valeurs k possibles prises par cette variable aléatoire et leur probabilité associée \(\mathbb P(X=k)\).
Exemple : Un dé à 6 faces
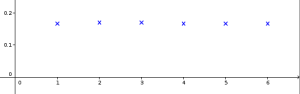
On lance un dé bien équilibré et on note X le numéro de la face obtenue. La variable aléatoire X peut prendre toutes les valeurs entières 1, 2, 3, 4, 5 et 6.
La loi de probabilité associée se résume dans le tableau
k | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
\(\mathbb P(X=k)\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) |
Graphiquement, on peut représenter cette loi de probabilité de la variable aléatoire discrète X par un nuage de points isolés dont la somme des ordonnées vaut 1.
Exemple : Un nombre aléatoire entre 0 et 6
Supposons à présent que l'on fabrique avec un tableur (ou la calculatrice) un nombre réel aléatoire entre 0 et 6 (au moyen de la fonction \(\fbox{=ALEA()*6}\) par exemple). Le nombre résultant de cette expérience constitue une variable aléatoire Y qui peut prendre toutes les valeurs entre 0 et 6.
La variable aléatoire Y est dite continue, par opposition à la variable aléatoire discrète X.
On peut se demander quelle est la probabilité que Y prenne une valeur comprise entre 0 et 3 ?
Intuitivement, on voit que plus l'intervalle cible est large, plus cette probabilité sera importante.
Ici, la largeur de l'intervalle cible est la moitié de l'intervalle contenant toutes les valeurs possibles de notre nombre aléatoire. On se dit donc qu'il y a une chance sur 2 pour que le nombre aléatoire se trouve entre 0 et 3, ce que l'on peut écrire \(\mathbb P(0\leqslant Y\leqslant 3)=\dfrac{1}{2}\)
On peut de même comprendre que \(\mathbb P(1\leqslant Y\leqslant 4)=\dfrac{1}{2}\) également puisque l'intervalle \([1 ;4]\) a la même largeur que l'intervalle \([0 ;3]\) et que nos nombres aléatoires sont uniformément répartis sur l'intervalle \([0 ;6]\)
Maintenant si on considère que l'intervalle cible possède une largeur égale au sixième de l'intervalle \([0 ;6]\) (comme par exemple \([1 ;2]\) ou \([4,5 ; 5,5]\)) on peut prévoir une probabilité que Y soit dans cet intervalle égale à \(\frac{1}{6}\).
Et en généralisant cela, on peut dire que si \(a,b\in[0 ;6]\) \(\mathbb P(a\leqslant Y\leqslant b)=\dfrac{b-a}{6}\)
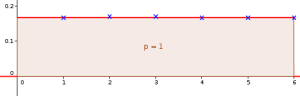
On vérifie alors que la probabilité que le nombre aléatoire soit compris entre 0 et 6 se calcule par :
\(\mathbb P(0\leq Y\leq 6)=\frac{6-0}{6}=1\)
Ce qui est conforme à ce que l'on attend puisqu'il s'agit ici de la probabilité de l'événement certain.
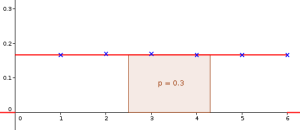
Si on interprète graphiquement cette expérience, on peut s'appuyer sur la fonction constante \(f(x)=\frac{1}{6}\) sur l'intervalle \([0 ;6]\). La probabilité qu'un nombre aléatoire compris entre 0 et 6 soit compris entre 2,5 et 4,3 correspond à l'aire du domaine délimité par les droites \(x=2,5\) et \(x=4,3\) d'une part, l'axe des abscisses et la fonction \(f\) d'autre part. En d'autres termes, on a :
\(\mathbb P(2,5\leq Y\leq 4,3)=\displaystyle \int_{2,5}^{4,3}f(x)~dx=\dfrac{1}{6}(4,3-2,5)=0,3\)
La fonction \(f\) n'a pas été choisie n'importe comment. Elle doit vérifier pour être cohérente avec notre expérience :
\(\displaystyle \int_{0}^{6}f(x)~dx=1\) puisque toutes les valeurs de Y sont entre 0 et 6.
Complément : Une conséquence étonnante des lois continues
Dans l'exemple précédent, considérons des intervalles de largeur de plus en plus petite : par exemple \(I_n=\left[2-\frac{1}{n} ;2+\dfrac{1}{n}\right]\)
La formule précédente nous montre que \(\mathbb P(Y\in I_n)=\dfrac{2/n}{6}=\frac{2}{6n}\)
Lorsque n devient grand :
l'événement \((Y\in I_n)\) se "rapproche" de l'événement \(Y=2\) puisque \(\dfrac{1}{n}\) tend vers 0 : l'amplitude de l'intervalle \(I_n\) tend vers 0,
la probabilité \(\frac{2}{6n}\) de cet événement tend vers 0.
On peut donc en conclure que \(\mathbb P(Y=2)=0\) ! !
Le passage au continu possède donc une conséquence surprenante :
La probabilité d'un nombre en particulier, par exemple la probabilité d'obtenir 2 exactement, est égale à 0 car il y a une infinité de nombres possibles et un seul réalise l'événement \((Y=2)\). On a ainsi \(\mathbb P(Y=2)=0\)
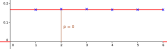
On peut aussi justifier ce résultat par :
\(\mathbb P(Y=2)=\displaystyle \int_{2}^{2}f(x)~dx=\dfrac{1}{6}(2-2)=0\)
Remarque : De la difficulté de simuler une loi continue avec une machine
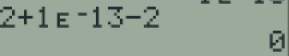
Par conséquent, il est impossible de deviner à l'avance le nombre exact qui sera pris par la variable aléatoire Y.
Si Y est simulée à l'aide d'une calculatrice, on peut obtenir un résultat un peu différent dans la mesure où la calculatrice ne possède pas une précision de calcul infinie comme le montre cette capture effectuée sur une TI83.
Ainsi pour la TI, dans les calculs, tout nombre dans l'intervalle \(\left[2-10^{-13} ;2+10^{-13}\right]\) sera assimilé à 2.
Pour la calculatrice, les événements \(Y=2\) et \(Y\in \left[2-10^{-13} ;2+10^{-13}\right]\) sont indiscernables du fait de la précision de calcul.
Pour le mathématicien par contre, \(\mathbb P(Y=2)=0\) mais \(P\left(Y\in \left[2-10^{-13} ;2+10^{-13}\right]\right)=\frac{2\cdot 10^{-13}}{6}\neq 0\)
Il est donc possible de deviner la valeur prise par Y lorsque celle-ci est simulée par la calculatrice, mais avec une probabilité très faible...
La calculatrice - ou les ordinateurs - ne vont donc pas simuler des variables aléatoires continues mais des variables aléatoires discrètes prenant beaucoup de valeurs possibles et se rapprochant donc ainsi du continu, sans toutefois atteindre la perfection.
Dans la suite, on supposera que les simulations effectuées avec la fonction ALEA() ou Random simulent une loi continue.