Première approche par la Loi Binomiale
On considère une variable aléatoire X suivant une loi binomiale de paramètres \(n\) et \(p\) :
\(X \hookrightarrow \mathcal B(n ;p)\)
On se rappelle que son espérance est \(\mathbb E(X)=n\times p\). On notera cette espérance \(\mu_X=n~p\)
On admettra également le résultat suivant : L'écart type d'une loi binomiale \(\mathcal B(n ;p)\) est \(\sigma_X=\sqrt{np(1-p)}\).
Simulation :
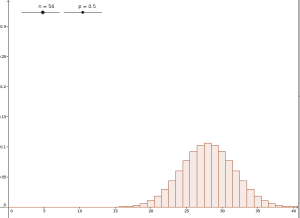
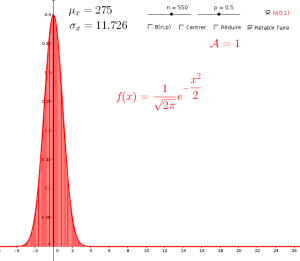
En observant cette simulation geogebra, on constate que lorsque n varie, l'histogramme représentant la loi binomiale se déplace du fait que l'abscisse du sommet de la cloche valant approximativement son espérance, augmente avec n. Cela est très gênant car nous allons tenter de passer du discret au continu et pour ce faire, répéter un grand nombre de fois l'expérience aléatoire en faisant tendre n vers l'infini, donc la cloche va s'éloigner vers la droite.
Pour contourner cette difficulté, nous allons centrer la variable aléatoire X en créant une nouvelle variable aléatoire \(Y=X-\mu_X\) obtenue en retranchant à X son espérance \(\mu_X=\mathbb E(X)\).
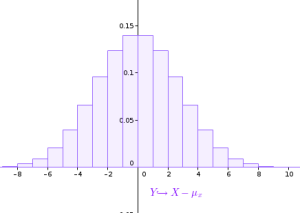
A présent, on constate que lorsque n augmente, la position du graphique reste centrée mais s'étale de plus en plus. Cela est du à l'écart type \(\sigma_X=\sqrt{np(1-p)}\) qui augmente avec n. L'idée pour normaliser la largeur du graphique va être de diviser Y par l'écart type et ainsi créer une nouvelle variable aléatoire Z définie par \(Z=\dfrac{X-\mu_X}{\sigma_X}\).
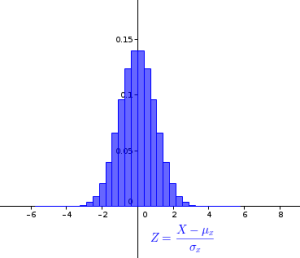
La nouvelle variable Z est nommé variable centrée réduite :
Son espérance vaut 0 et son écart-type vaut 1. cf act p 193
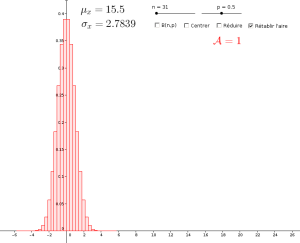
Hélas en faisant cette opération l'aire totale des rectangles a été modifiée car la largeur divisée par \(\sigma_X\). Afin de retrouver une aire totale de 1 et ainsi nécessaire pour obtenir une loi de probabilité, nous allons devoir multiplier la hauteur des rectangles par \(\sigma_X\) afin de compenser la diminution de largeur. Nous obtenons ainsi l'histogramme rouge dont l'aire vaut 1 et qui est centré et réduit autour de l'origine.
Vous pouvez reproduire les différentes étapes amenant à cette construction à laide de la simulation suivante. Faites ensuite l'expérience d'augmenter la valeur de n afin de simuler le passage d'une loi discrète à une loi continue.
Fondamental : Du discret au continu
Lorsque n devient grand, notre loi binomiale centrée réduite et normalisée forme une courbe en cloche qui coïncide avec la fonction
\(f(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\dfrac{x^2}{2}}\).
Ce résultat a été découvert par le mathématicien français Abraham de Moivre (1667, Vitry-le-François – 1754, Londres) :
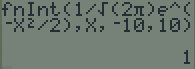
L'aire sous cette courbe est égale à 1 car nous avons construit l'histogramme rouge de manière à conserver une aire totale de 1. Nous pouvons utiliser la fonction intégrale de la calculatrice pour vérifier ce résultat.
Attention :
La fonction \(f(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\dfrac{x^2}{2}}\) admet des primitives mais il est impossible de les exprimer explicitement au moyen des fonctions usuelles. Nous avons donc recours pour calculer les intégrales à des méthodes de calcul numérique approché.
L'aire sous la courbe est très très faible pour des valeurs de x grandes car la courbe s'écrase sur l'axe des abscisses. Nous obtenons donc une approximation de l'aire totale sous la courbe en utilisant une intégrale sur l'intervalle [-10 ;10] car la calculatrice ne sait pas calculer jusqu'à l'infini.
Définition : Gaussienne
La fonction \(f(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\dfrac{x^2}{2}}\) est appelée fonction de gauss, du nom du mathématicien qui l'a découverte.