Calcul de u alpha à la calculatrice
Simulation :
La simulation suivante montre graphiquement l'influence de la modification du paramètre \(\alpha\) sur la détermination de \(u_\alpha\)
On s'intéressera à la probabilité \(\mathbb P(X\leqslant u_\alpha)\) : On comprend sur le graphique que l'on a bien
\(\mathbb P(X\leqslant u_\alpha)=1-\dfrac{\alpha}{2}\)
Méthode : Détermination de u alpha à la calculatrice
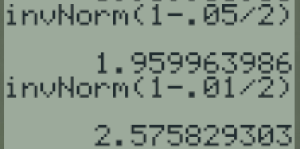
La fonction InvNorm(p) de la calculatrice retourne le nombre x tel que \(\mathbb P(X\leqslant x)=p\)
Étant donné \(\alpha\), on calcule \(p=1-\dfrac{\alpha}{2}\)
Puis la calculatrice nous donne \(u_\alpha\) par la fonction InvNorm(p)
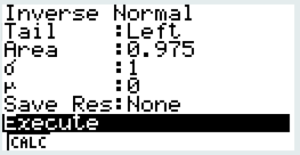
Calcul sur TI.
La fonction invNorm se trouve dans le menu \(\fbox{2nde}~\fbox{distrib}\)
Calcul sur Casio
La fonction iNorm se trouve dans le menu stats sous \(\fbox{DIST}~\fbox {F3}\) iNorm
Pour appliquer la même méthode que sur TI, on positionne la queue tail sur left.
On pourrait obtenir le même résultat (ici 
) en
positionnant Tail sur Center et plaçant 0,95 pour Area
positionnant Tail sur Right et plaçant 0,275 pour Area
Un examen de la simulation géogébra est parlant par rapport à ces données. A chacun de déterminer sa méthode préférée, mais attention de bien vérifier la position du champ Tail par rapport aux données que vous introduisez ! ! !
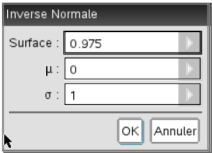
Calcul sur nSpire
La fonction Inverse Normale se trouve dans le
\(\fbox{Menu}\) 5 :Probabilités 5 : Distributions 3 : Inverse Normale
On paramétrera les champs de saisie comme ci-contre.
On peut également taper directement la commande
Fondamental :
On retiendra les deux valeurs suivantes :
\(u_{0,05}\approx 1,96\)
\(u_{0,01}\approx 2,58\)