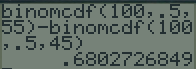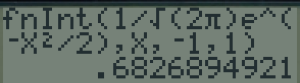Application au calcul des grandes binomiales
On considère une variable aléatoire X suivant une loi binomiale de paramètres 100 et 0,5 : \(X \hookrightarrow \mathcal B(100 ;0.5)\)
On s'intéresse à \(\mathbb P(45< X\leqslant 55)\).
Question
Calculer l'espérance \(\mu_X\) et l'écart type \(\sigma_X\) de X.
Solution
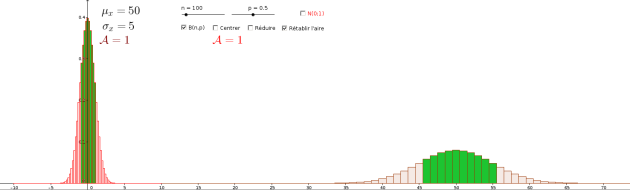
On sait que \(E(X)=n\times p\) donc \(\mu_X=100\times 0,5=50\)
De même l'écart type \(\sigma_X=\sqrt{n p(1-p)}=\sqrt{100\times 0,5\times 0.5}=\sqrt{25}=5\)
Question
On définit la variable aléatoire Z centrée réduite de X par \(Z=\dfrac{X-\mu_X}{\sigma_X}\).
Expliquer pourquoi \(\mathbb P(45< X\leqslant 55)=\mathbb P(-1< Z\leqslant 1)\)
Indice
Si \(X\) prend ses valeurs entre 45 et 55, entre quels nombres \(Z\) prendra t-il ses valeurs ?
Solution
On a \(~~\dfrac{45-\mu_X}{\sigma_X}=\dfrac{45-50}{5}=-1\)
et \(~~\dfrac{55-\sigma_X}{\sigma_X}=\dfrac{55-50}{5}=1\)
L'opération de centrage ne change pas les aires (simple translation). L'opération de normalisation ne les change pas non plus car la largeur des rectangles est divisée par 5 mais la hauteur est multipliée par 5 et donc au final l'aire est conservée.
On en conclut que les aires représentées en vert sur les deux graphiques sont identiques.
Par conséquent, \(\mathbb P(45< X\leqslant 55)=\mathbb P(-1< Z\leqslant 1)\)
Question
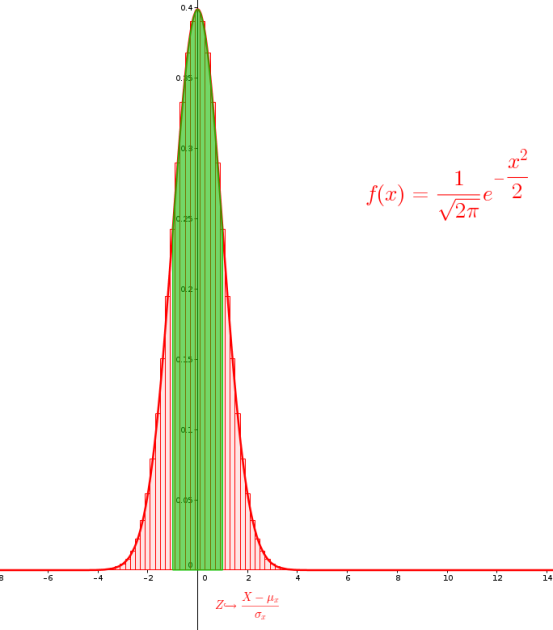
Expliquer pourquoi \(\mathbb P(45< X\leqslant 55)\) peut être approchée par \(\displaystyle \int_{-1}^1 ~\dfrac{1}{\sqrt{2\pi}}e^{-\dfrac{x^2}{2}} ~dx\)
Indice
On remarquera que 100 est un nombre assez grand...
Solution
La loi binomiale centrée réduite s'approche beaucoup de la courbe de Gauss lorsque n est assez grand. Par conséquent, il y a très peu de différence entre \(\mathbb P(-1< Z\leqslant 1)\) et l'aire sous la courbe de gauss pour x compris entre -1 et 1.
Par conséquent, \(\mathbb P(45< X\leqslant 55)=\mathbb P(-1< Z\leqslant 1)\approx \displaystyle \int_{-1}^1 ~\dfrac{1}{\sqrt{2\pi}}e^{-\dfrac{x^2}{2}} ~dx\)
Remarque :
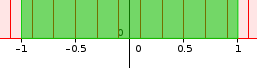
En zoomant sur l'intégrale, on remarque que les bornes de l'intégrale coupent les rectangles du bord en deux (voir ci-contre). De ce fait, le rectangle de droite qui correspond à \((X=55)\) est compté à moitié et le rectangle de gauche qui correspond à \((X=45)\) est également compté à moitié. Cela revient à dire que l'on compte totalement le rectangle de droite \((X=55)\) et pas du tout le rectangle de gauche \((X=45)\).
Cela explique pourquoi dans la probabilité, on a exclu 45 et on inclut 55.
Question
Calculer à la calculatrice :
\(\mathbb P(45< X\leqslant 55)\)
\(\displaystyle \int_{-1}^1 ~\dfrac{1}{\sqrt{2\pi}}e^{-\dfrac{x^2}{2}} ~dx\)
et donner une estimation de l'erreur commise par l'approximation de la loi binomiale par l'intégrale.
Indice
On révisera l'utilisation de la calculatrice pour la loi binomiale et pour le calcul des intégrales.
\(\mathbb P(45< X\leqslant 55)=\mathbb P(X\leqslant 55)-\mathbb P(X\leqslant 45)\)
Solution
\(\mathbb P(45< X\leqslant 55)\approx 0.68027\)
\(\displaystyle \int_{-1}^1 ~\dfrac{1}{\sqrt{2\pi}}e^{-\dfrac{x^2}{2}} ~dx\approx 0,68269\)
L'erreur commise en approximant la loi binomiale par l'intégrale de la fonction de Gauss est donc ici de 0,0024, soit de l'ordre de deux millièmes, ce qui est très peu.
Conclusion
Par conséquent on considère que pour les grandes binomiales, l'intégrale de la courbe de Gauss fournir une assez bonne approximation de la loi binomiale.
Ce résultat est dû à Abraham de Moivre qui fait apparaître pour la première fois en 1756 la loi normale comme limite d'une loi binomiale.