Probabilités composées
On sait que si A et B sont deux événements, A étant possible, \(P_A(B)=\dfrac{P(A\cap B)}{P(A)}\). En multipliant cette égalité par \(P(A)\) non nul, on en déduit la formule suivante :
Fondamental :
Si l'on connaît la probabilité de l'événement A et la probabilité de l'événement B sachant que A est réalisé, la probabilité de l'événement \(A\cap B\) est \(P(A\cap B)=P(A)\times P_A(B)\)
Exemple :
Un joueur de tennis réussit sa première balle de service à 75% et sa deuxième balle à 90%. Quelle est la probabilité qu'il commette une double faute ?
Si l'événement A est "le joueur rate sa première balle".
On sait d'après l'énoncé que \(P(A)=1-0,75=0,25\).
L'événement B est "Le joueur rate sa seconde balle"et l’événement \(\bar{B}\) est "Le joueur réussit sa deuxième balle".
L'événement B sachant A est "le joueur rate sa seconde balle sachant qu'il a raté la première également".
On a d'après l'énoncé que \(P_A(B)=1-P_A(\bar{B})=1-0,9=0,1\)
La double faute est l'événement \(A\cap B\). Or \(P(A\cap B)=P(A)\times P_A(B)=0,25\times 0,1=0,025\)
La probabilité que le joueur rate ses deux services est de 0,025.
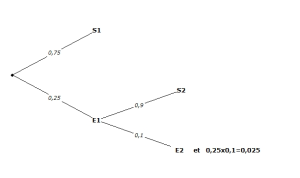
Visuellement cette situation se représente aisément à l'aide d'un arbre pondéré.
E1 et S1 représentent successivement l'échec et le succès au premier service.
E2 et S2 représentent successivement l'échec et le succès au second service.
On constate que la probabilité d'avoir une double faute correspond à la probabilité de la feuille E2. Celle-ci s'obtient d'après la formule précédente en faisant le produit des probabilités des branches menant à cette feuille.
Remarque :
Si \(P(A)\neq0\) et \(P(B)\neq0\), on a :
\(P(A\cap B)=P(A) \times P_A(B) =P(B) \times P_B(A)\)