Construire et utiliser un arbre pondéré
A la session 2009 du Bac, 286 762 élèves inscrits en série générale ont été admis. En particulier 47 765 en série L, 90 466 en série ES et 148 531 en série S. Le tableau suivant présente la proportion de bacheliers ayant obtenu une mention :
Mention Assez Bien | Mention Bien ou Très Bien | |
Série L | 27,3% | 16,1% |
Série ES | 28,8% | 15,3% |
Série S | 29,2% | 30,9% |
On interroge au hasard un bachelier en série générale de cette session 2009.
Question
Construire un arbre pondéré traduisant la situation. On utilisera les notations suivantes :
L : événement "le bachelier a suivi la filière L"
E : événement "le bachelier a suivi la filière ES"
S : événement "le bachelier a suivi la filière S"
R : événement "le bachelier a été reçu sans mention"
A : événement "le bachelier a éré reçu mention AB"
B : événement "le bachelier a été reçu mention B ou TB"
On arrondira les probabilités au millième près.
Indice
Calculer P(L), P(E) et P(S) en utilisant les effectifs fournis en introduction du problème.
Indice
Les éléments du tableau s'interprètent comme des probabilités conditionnelles. Ainsi par exemple la probabilité d'avoir obtenu Assez bien sachant qu'on a suivi la série L est 27,3% soit 0,273. Cela s'écrit \(P_L(A)=0,273\)
Indice
Connaissant les probabilités des mentions, il est facile par complément à 100% d'obtenir pour chaque filière les probabilités de l'événement R représentant les mentions passables.
Solution
L'arbre pondéré compte tenu des indications fournies ci-dessus s'obtient alors facilement en reportant les données du problème.
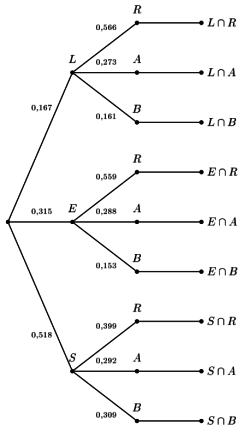
Question
Quelle est la probabilité qu'un bachelier interrogé au hasard ait obtenu une mention AB dans la série ES ?
Indice
L'événement correspondant à la question est \(E\cap A\).
Solution
\(P(E\cap A)=P(E)\times P_E(A)=0,315\times 0,288\approx 0,09\)
Visuellement sur l'arbre établi à la question précédente, on retrouve ce résultat en multipliant les probabilités des branches menant à la feuille \(E\cap A\).