Construction d'une fonction telle que f '= f et f(0)=1
Dans cette activité, nous cherchons à construire de manière approchée la courbe représentative d'une fonction dérivable f vérifiant :
\(f'=f\)
\(f(0)=1\)
Avec un pas de 1 :
Question
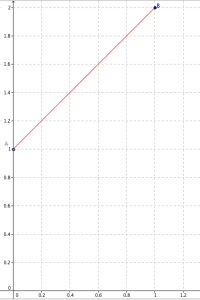
Quelle est l'équation de la tangente à la courbe au point d'abscisse 0 ?
Tracer le segment porté par cette tangente pour \(x\) variant de 0 à 1.
Si on assimile la courbe à sa tangente, quelle approximation peut-on donner de \(f(1)\) ?
Solution
\(y=f'(x_0)(x-x_0)+f(x_0)\)
Ici \(x_0=0\) et \(f'(0) =f(0)=1\)
Donc la tangente a pour équation : \(y=1(x-0)+1\)
Si on assimile la courbe à sa tangente sur [0 ;1], on obtient le tracé ci-contre.
On peut en déduire l'approximation \(f(1)\approx 1+1=2\).
Avec un pas de 0,5 :
On coupe à présent l'intervalle [0 ;1] en deux parties. En \(x=0,5\), on actualise la pente du segment de droite en fonction de la valeur approximative de \(f\).
Question
Avec la méthode utilisée précédemment,quelle approximation de f(0,5) obtient-on ? Qu'en déduit-on pour f'(0,5) ?
Donner une nouvelle approximation de \(f(1)\).
Solution
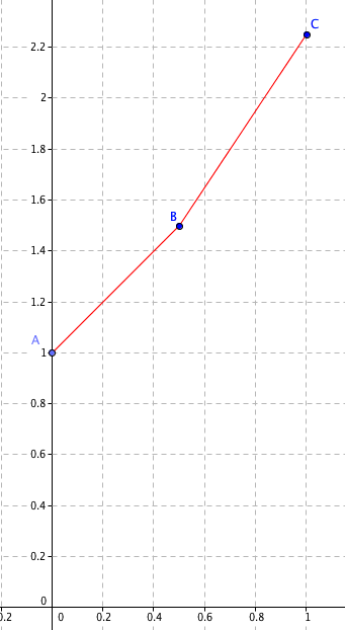
Le premier segment de droite $(d_1)$ a pour équation \(y=x+1\).
Pour \(x=0,5\), il fournit la valeur approximative \(f(0,5)=0,5+1=1,5\)
Maintenant, \(f'(0,5)=f(0,5)=1,5\).
La nouvelle tangente (d2) en 0,5 a donc pour pente 1,5.
L'équation de (d2) est \(y=f'(0,5)(x-0,5)+f(0,5)=1,5(x-0,5)+1,5\)
On en déduit que \(f(1)\) est le point d'abscisse 1 sur cette tangente a pour valeur approchée \(y=1,5(0,5)+1,5=2,25\)
Question
Supposons connues les cordonnées \(x_0\) et \(y_0\) d'un point de la courbe.
En supposant que sur un petit déplacement \(\Delta x\), la courbe de notre fonction mystère peut être assimilée à une droite, quelles sont les coordonnées du point d'abscisse \(x_0+\Delta x\) ?
Solution
\(f(x_0)=f'(x_0)\) donc la droite a pour coefficient directeur \(y_0\). Si on se déplace horizontalement de \(\Delta x\) on se déplace verticalement de \(y_0\times \Delta x\).
Le point d'abscisse \(x_0+\Delta x\) a donc pour ordonnée \(y_0+y_0\times \Delta x\).
Question
Reproduire la construction précédente avec un pas de 0,2 pour en déduire une valeur approchée de \(f(1)\).
Solution
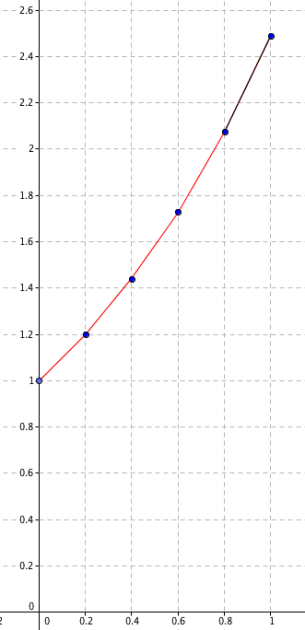
On place les points A(0 ;1) et B(0,2 ; 1,2) pour démarrer la construction.
En B, la tangente a pour pente 1,2. Si on avance de 0,2, on monte de 1,2*0,2 soit 0,24. On place le point C(0,4 ;1,44).
En C, la tangente a pour pente 1,44. Si on avance de 0,2, on monte de 1,44*0,2 soit 0,288. On place le point D(0,6 ;1,728).
En D, la tangente a pour pente 1,728. Si on avance de 0,2, on monte de 1,728*0,2 soit 0,3456. On place le point E(0,8 ;2,0736).
En E, la tangente a pour pente 2,0736. Si on avance de 0,2, on monte de 2,0736*0,2 soit 0,41472. On place le point F(1 ;2,48832).
Pour cette dernière construction, on obtient une approximation de \(f(1)\approx 2,49\).
Bilan de l'activité
On voit ainsi qu'il semble possible de proche en proche de construire une telle fonction vérifiant les deux contraintes données au départ. Plus on affine le pas, plus la courbe devient lisse et se dresse peu à peu.
L'animation ci-dessous permet de montrer les 3 constructions que nous avons réalisé, et d'y superposer la courbe finale de notre fonction mystère que nous appellerons exp