Utiliser les théorèmes de comparaison pour calculer des limites.
Question
Calculer \(\lim\limits_{x \to +\infty} x^3+x\cos x\)
Indice
On pourra remarquer que \(cos(x)\geqslant -1\) pour tout \(x\in \mathbb R\)
Indice
Calculer \(\lim\limits_{x \to +\infty} x^3- x\)
Solution
On sait que pour tout \(x\in \mathbb R, \cos(x)\geqslant -1\)
Donc si \(x>0, x\cos x\geqslant -x\)
Donc au voisinage de +∞, on a \(x^3+x\cos x \geqslant x^3-x\)
Calculons à présent \(\lim\limits_{x \to +\infty} x^3- x\)
Méthode : Lever l'indétermination
Pour lever l'indétermination ∞-∞, on met le terme dominant \(x^3\) en facteur :
\(x^3-x=x^3\left(1-\frac{x}{x^3}\right)=x^3\left(1-\frac{1}{x^2}\right)\)
Or \(\lim\limits_{x \to +\infty} \frac{1}{x^2}=0\) donc \(\lim\limits_{x \to +\infty} 1-\frac{1}{x^2}=1\)
De plus \(\lim\limits_{x \to +\infty} x^3=+\infty\)
Donc par la règle du produit des limites \(\lim\limits_{x \to +\infty} x^3-x=+\infty\)
Méthode : Appliquer le théorème de comparaison
On sait donc que
Pour tout \(x>0\), \( x^3+x\cos x \geqslant x^3-x\)
De plus \(\lim\limits_{x \to +\infty} x^3-x=+\infty\)
D'après le théorème de comparaison on peut affirmer que \(\lim\limits_{x \to +\infty} x^3+x\cos x=+\infty\)
Question
Calculer \(\lim\limits_{x \to +\infty} ~\frac{x\cos x}{x^2+1}\)
Indice
On pourra remarquer que \(-1\leqslant \cos(x)\leqslant 1\) pour tout \(x\in \mathbb R\)
Indice
On pourra calculer les limites suivantes :
\(\lim\limits_{x \to +\infty} \frac{-x}{x^2+1}\)
\(\lim\limits_{x \to +\infty} \frac{x}{x^2+1}\)
Solution
On sait que \(-1\leqslant \cos(x)\leqslant 1\) pour tout \(x\in \mathbb R\)
donc si \(x>0\), \(-x\leqslant x\cos x\leqslant x\)
en divisant par \(x^2+1>0\), on obtient alors l'encadrement suivant :
Pour tout \(x>0\), \( \frac{- x}{x^2+1}\leqslant \frac{x\cos x}{x^2+1}\leqslant \frac{x}{x^2+1}\)
Calculons \(\lim\limits_{x \to +\infty} \frac{x}{x^2+1}\)
Méthode : Lever l'indétermination
On va simplifier la fraction en mettant en facteur au dénominateur le terme dominant :
\(\frac{x}{x^2+1}=\frac{x}{x^2\left(1+\frac{1}{x^2}\right)}=\frac{1}{x\left(1+\frac{1}{x^2}\right)}\) en simplifiant par \(x\).
Or \(\lim\limits_{x \to +\infty} 1+\frac{1}{x^2}=1\) donc \(\lim\limits_{x \to +\infty}x\left(1+\frac{1}{x^2}\right)=+\infty\)
Par passage à l'inverse, on obtient une limite nulle.
donc \(\lim\limits_{x \to +\infty} \frac{x}{x^2+1}=0\)
On en déduit également par passage à l'opposé que \(\lim\limits_{x \to +\infty} \frac{-x}{x^2+1}=0\)
Méthode : Utiliser le théorème des gendarmes
On sait donc que
Pour tout \(x>0\),\( \frac{- x}{x^2+1}\leqslant \frac{x\cos x}{x^2+1}\leqslant \frac{x}{x^2+1}\)
\(\lim\limits_{x \to +\infty} \frac{x}{x^2+1}=\lim\limits_{x \to +\infty} \frac{-x}{x^2+1}=0\)
Donc en appliquant le théorème des gendarmes, on en déduit que :
\(\lim\limits_{x \to +\infty} ~\frac{x\cos x}{x^2+1}=0\)
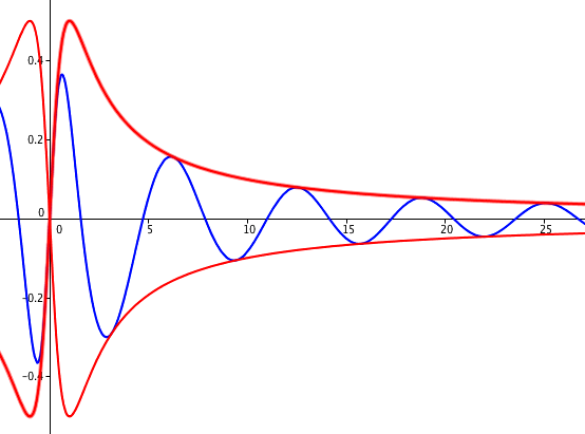
Voici graphiquement l'interprétation de ces calculs. On voit assez nettement la fonction de départ en bleu encadrée par les deux "gendarmes" en rouge qui la forcent à tendre vers 0.